Puzzle time - the Fibonacci numbers

jon-nyc

I use 8086 assembler for such tasks.

Doctor Phibes

Are you two about to have a 'my dick is smaller' contest?

Klaus

@Doctor-Phibes Did you know that dick sizes have a Fibonacci distribution? It's a distribution with a very long tail...

jon-nyc

@jon-nyc said in Puzzle time - the Fibonacci numbers:

Interesting observation:

Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?

bump for Klaus and his little 4 line program.

Klaus

@jon-nyc said in Puzzle time - the Fibonacci numbers:

@jon-nyc said in Puzzle time - the Fibonacci numbers:

Interesting observation:

Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?

bump for Klaus and his little 4 line program.

Can you explain? You mean that the cycle length of Fib mod (2^n) is the same as Fib mod (3*2^(n-1))? That doesn't seem to be true.

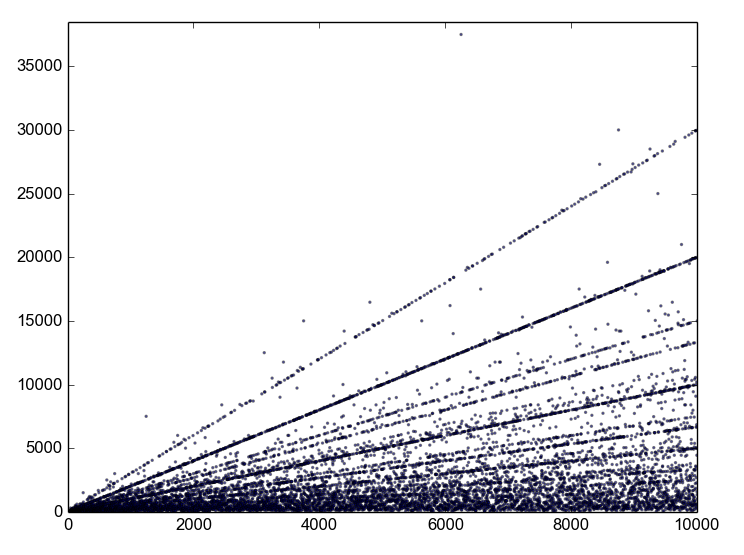
I uploaded the first 10,000 cycle lengths here, if you want to check this yourself.
https://www.heypasteit.com/clip/0IV18W

jon-nyc

No, the cycle length of Fib mod (2^n) = 3*2^(n-1))

Check Fmod2, Fmod4, Fmod8, Fmod16 etc for their cycle lengths. You’ll get 3,6,12,24,48 etc. I’m wondering if it holds. I think it will.

Klaus

Here's a list of pairs where the first number shows the "n" (but only for powers of 2) and the second one the associated cycle length. Maybe I missunderstood something but your conjecture doesn't seem to hold.

[(2,6),(4,24),(8,60),(16,24),(32,36),(64,120),(128,420),(256,264),(512,516),(1024,72),(2048,600),(4096,1368),(8192,720)]

jon-nyc

But your original list is this one:

(left side numbering mine, right side list yours)

Klaus

Ah, looks like an "off by two" error somewhere. Hmm....

Klaus

Turned out to be two "off by 1" errors that have to do with indices starting at 0 and not 1.

What about this result?

[(2,3),(4,6),(8,12),(16,24),(32,48),(64,96),(128,192),(256,384),(512,768),(1024,1536),(2048,3072),(4096,6144),(8192,12288)]

Klaus

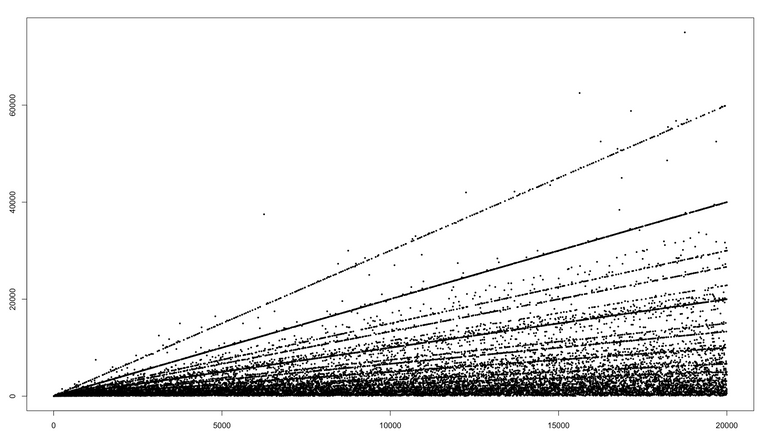
It looks like linear relations between the cycle length happen quite frequently. This is a scatter plot of the cycle lengths I computed above (haven't used R in a while - fun for plotting data!). Observe all the dotted lines. The points you identified are on one of those lines. Also interesting to see a few outliers.

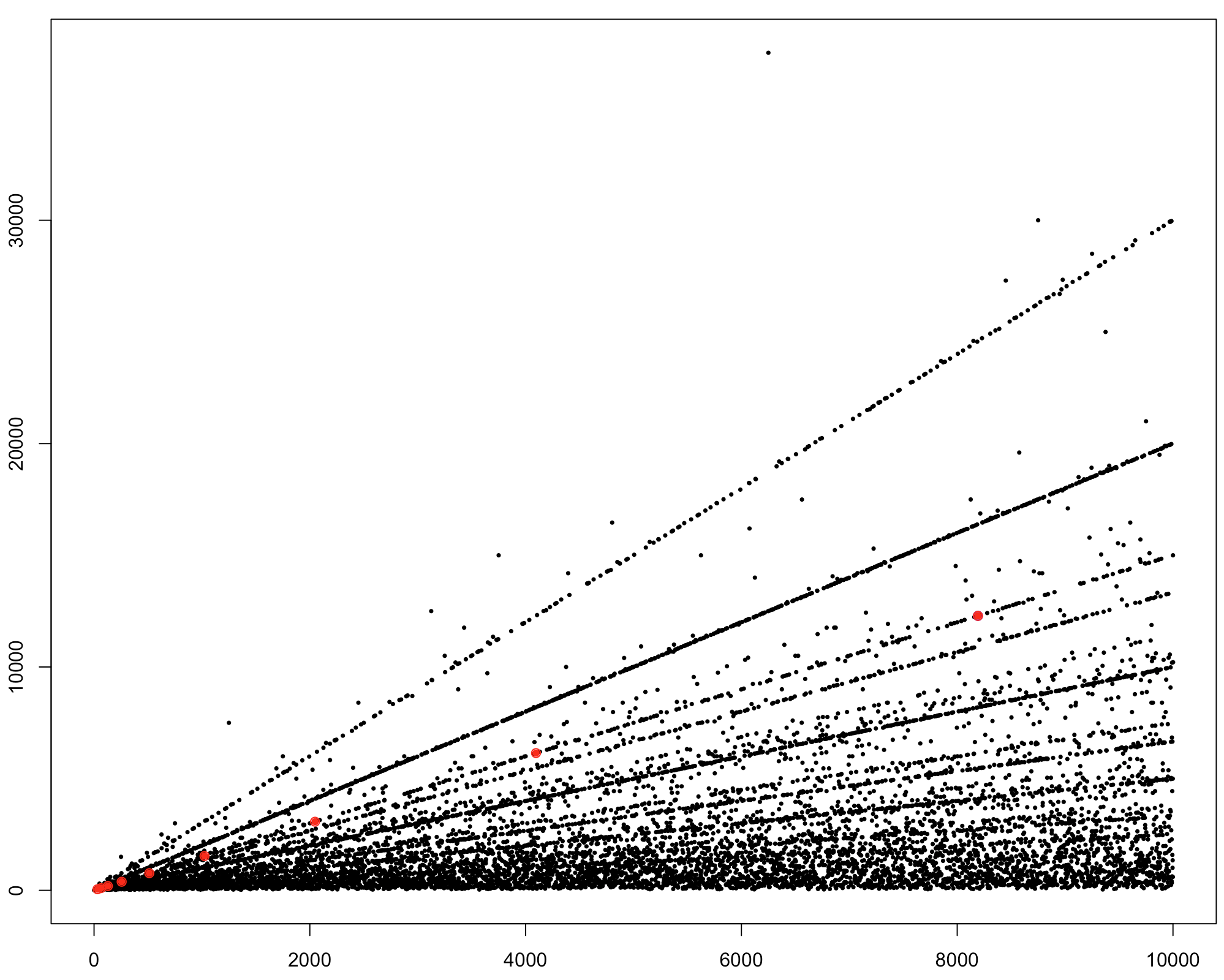
I have marked the points you are interested in in red. You see that there are way more points on that line.

jon-nyc

Interesting.

So it turns out Fibonacci cycle lengths a thing people study. They’re called Pisano numbers and understanding them is really about understanding Pisano numbers for prime powers.

A neat property is that if n and m are coprime then period(mn) is least common multiple of period(n) and period(m).

jon-nyc

Wait a minute, is that really your graph up there? This is from Wiki

Klaus

Yes, it's my graph. I haven't seen the WIki graph yet, but it shows the same data, so of course it's similar. It's an interesting coincidence that they also cut off at 10,000.

Klaus

Just for fun, here's the continuation of the dataset for cycle lengths up to 20000.

The New Coffee Room

Puzzle time - the Fibonacci numbers