Puzzle time - the Fibonacci numbers
-
Well, the "mod n" sequences seem to loop. In particular, they always seem to come back to 0. Which means that those "0" points can be divided by n.
So if "zero(n)" is the index of the first fibonacci number (different from 0) where Fib(zero(n)) mod n = 0, then n divides the zero(n)-th Fibonacci number.
However, it's not so clear why the "mod n" sequences have that looping structure.
-
I think the proof of looping can be seen from the congruence property of modular arithmetic. In particular, "modulo" is a congruence with respect to Fibonacci numbers:
Fib(n) mod m = (Fib(n-1) mod m) + (Fib(n-2) mod m) (for n >= 2)
Since there are only about m^2 possible pairs of numbers in the "mod n" ring, and Fib(n) mod m only depends on the pair of previous numbers (mod m), it follows that the sequence must necessarily loop.
-
I did a tiny bit of programming, and I think it's a nice programming exercise to come up with an elegant way to compute the cycle length of "Fib mod n" sequences.
Here's a 4-liner I came up with.
fibsmod n = map ((`mod` n) . fst) $ iterate (\(a,b) -> (b,a+b)) (0,1) pairIndex a b (x:y:ys) m = if (a == x) && (b == y) then m else pairIndex a b (y:ys) (m+1) p (x:y:ys) = pairIndex x y ys 2 take 100 $ map (p . fibsmod) [2..]It computes the first 100 cycle length:
[3,8,6,20,24,16,12,24,60,10,24,28,48,40,24,36,24,18,60,16,30,48,24,100,84,72,48,14,120,30,48,40,36,80,24,76,18,56,60,40,48,88,30,120,48,32,24,112,300,72,84,108,72,20,48,72,42,58,120,60,30,48,96,140,120,136,36,48,240,70,24,148,228,200,18,80,168,78,120,216,120,168,48,180,264,56,60,44,120,112,48,120,96,180,48,196,336,120,300,50] -
Are you two about to have a 'my dick is smaller' contest?
-
Are you two about to have a 'my dick is smaller' contest?
-
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
@jon-nyc said in Puzzle time - the Fibonacci numbers:
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
bump for Klaus and his little 4 line program.
-
@jon-nyc said in Puzzle time - the Fibonacci numbers:
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
bump for Klaus and his little 4 line program.
@jon-nyc said in Puzzle time - the Fibonacci numbers:
@jon-nyc said in Puzzle time - the Fibonacci numbers:
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
bump for Klaus and his little 4 line program.
Can you explain? You mean that the cycle length of Fib mod (2^n) is the same as Fib mod (3*2^(n-1))? That doesn't seem to be true.
I uploaded the first 10,000 cycle lengths here, if you want to check this yourself.
https://www.heypasteit.com/clip/0IV18W -
Here's a list of pairs where the first number shows the "n" (but only for powers of 2) and the second one the associated cycle length. Maybe I missunderstood something but your conjecture doesn't seem to hold.
[(2,6),(4,24),(8,60),(16,24),(32,36),(64,120),(128,420),(256,264),(512,516),(1024,72),(2048,600),(4096,1368),(8192,720)] -
-
It looks like linear relations between the cycle length happen quite frequently. This is a scatter plot of the cycle lengths I computed above (haven't used R in a while - fun for plotting data!). Observe all the dotted lines. The points you identified are on one of those lines. Also interesting to see a few outliers.
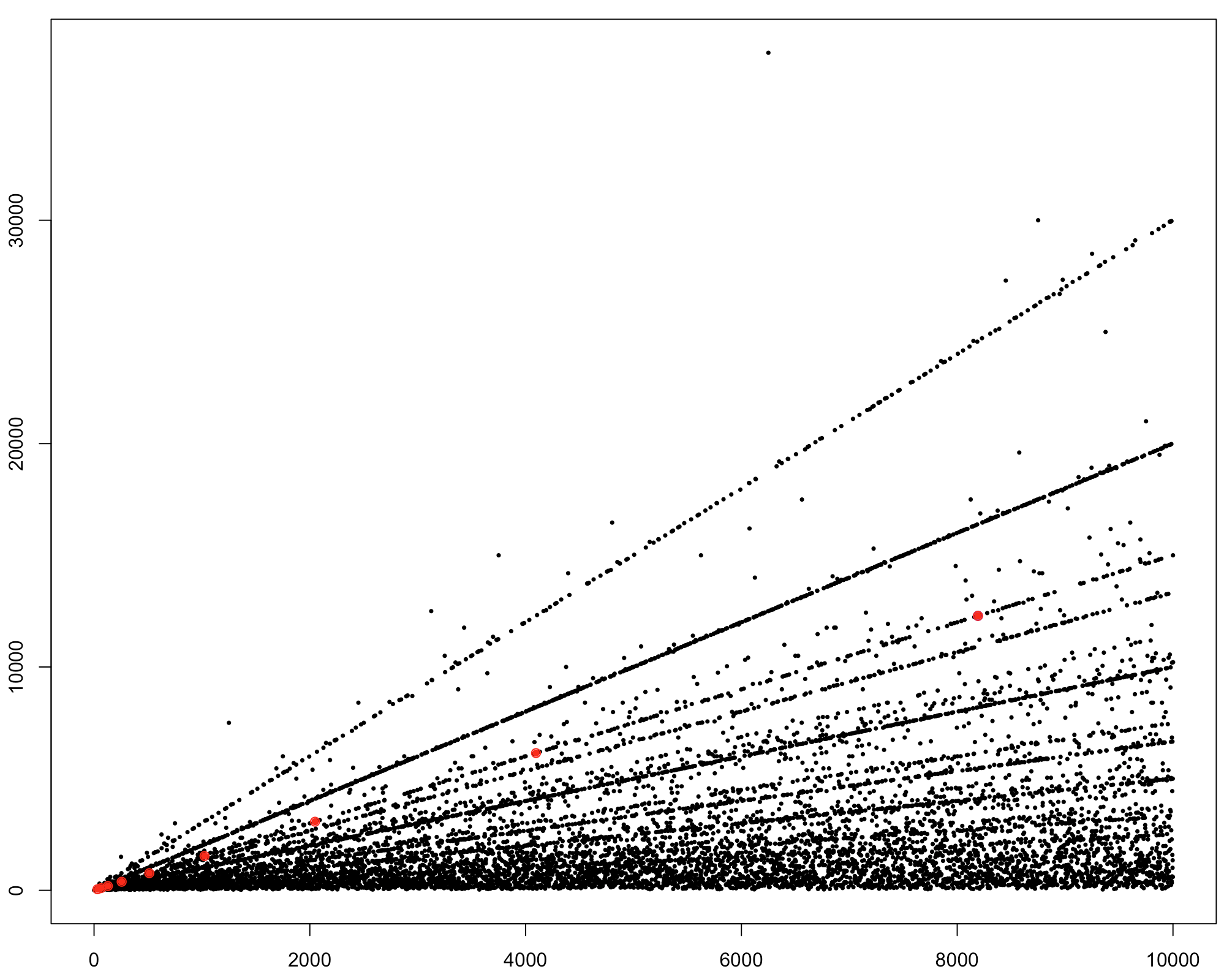
I have marked the points you are interested in in red. You see that there are way more points on that line.
