Puzzle time - the Fibonacci numbers
-
Are you two about to have a 'my dick is smaller' contest?
-
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
@jon-nyc said in Puzzle time - the Fibonacci numbers:
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
bump for Klaus and his little 4 line program.
-
@jon-nyc said in Puzzle time - the Fibonacci numbers:
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
bump for Klaus and his little 4 line program.
@jon-nyc said in Puzzle time - the Fibonacci numbers:
@jon-nyc said in Puzzle time - the Fibonacci numbers:
Interesting observation:
Cycle lengths 2^n = 3*2^(n-1) at least within the first 100. Does that continue?
bump for Klaus and his little 4 line program.
Can you explain? You mean that the cycle length of Fib mod (2^n) is the same as Fib mod (3*2^(n-1))? That doesn't seem to be true.
I uploaded the first 10,000 cycle lengths here, if you want to check this yourself.
https://www.heypasteit.com/clip/0IV18W -
Here's a list of pairs where the first number shows the "n" (but only for powers of 2) and the second one the associated cycle length. Maybe I missunderstood something but your conjecture doesn't seem to hold.
[(2,6),(4,24),(8,60),(16,24),(32,36),(64,120),(128,420),(256,264),(512,516),(1024,72),(2048,600),(4096,1368),(8192,720)] -
-
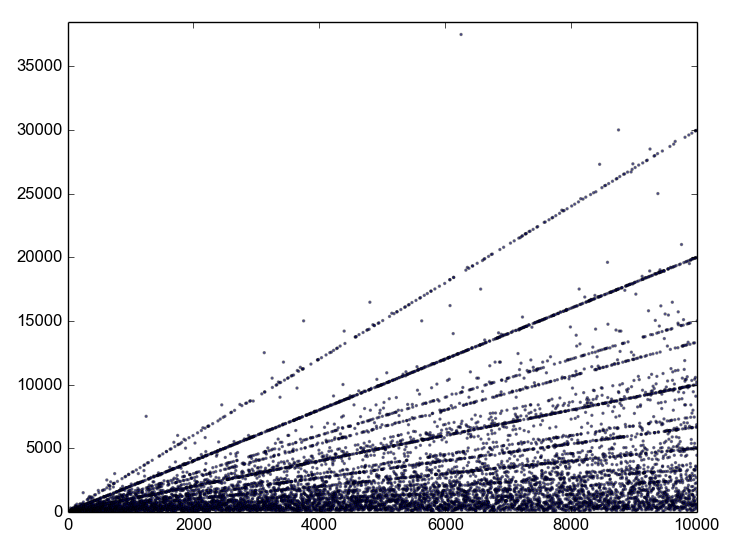
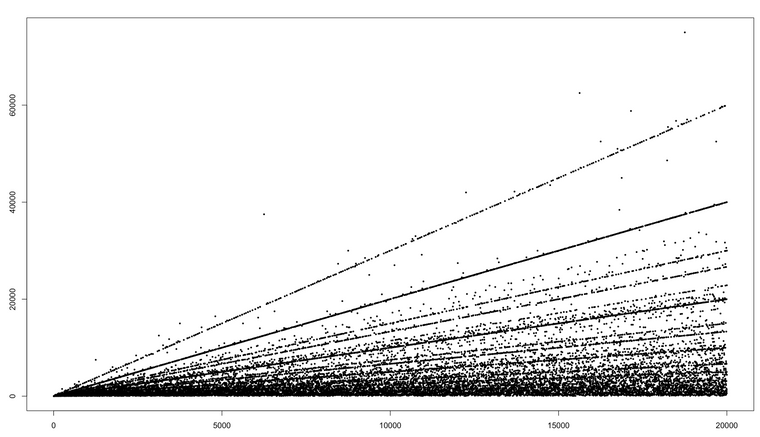
It looks like linear relations between the cycle length happen quite frequently. This is a scatter plot of the cycle lengths I computed above (haven't used R in a while - fun for plotting data!). Observe all the dotted lines. The points you identified are on one of those lines. Also interesting to see a few outliers.
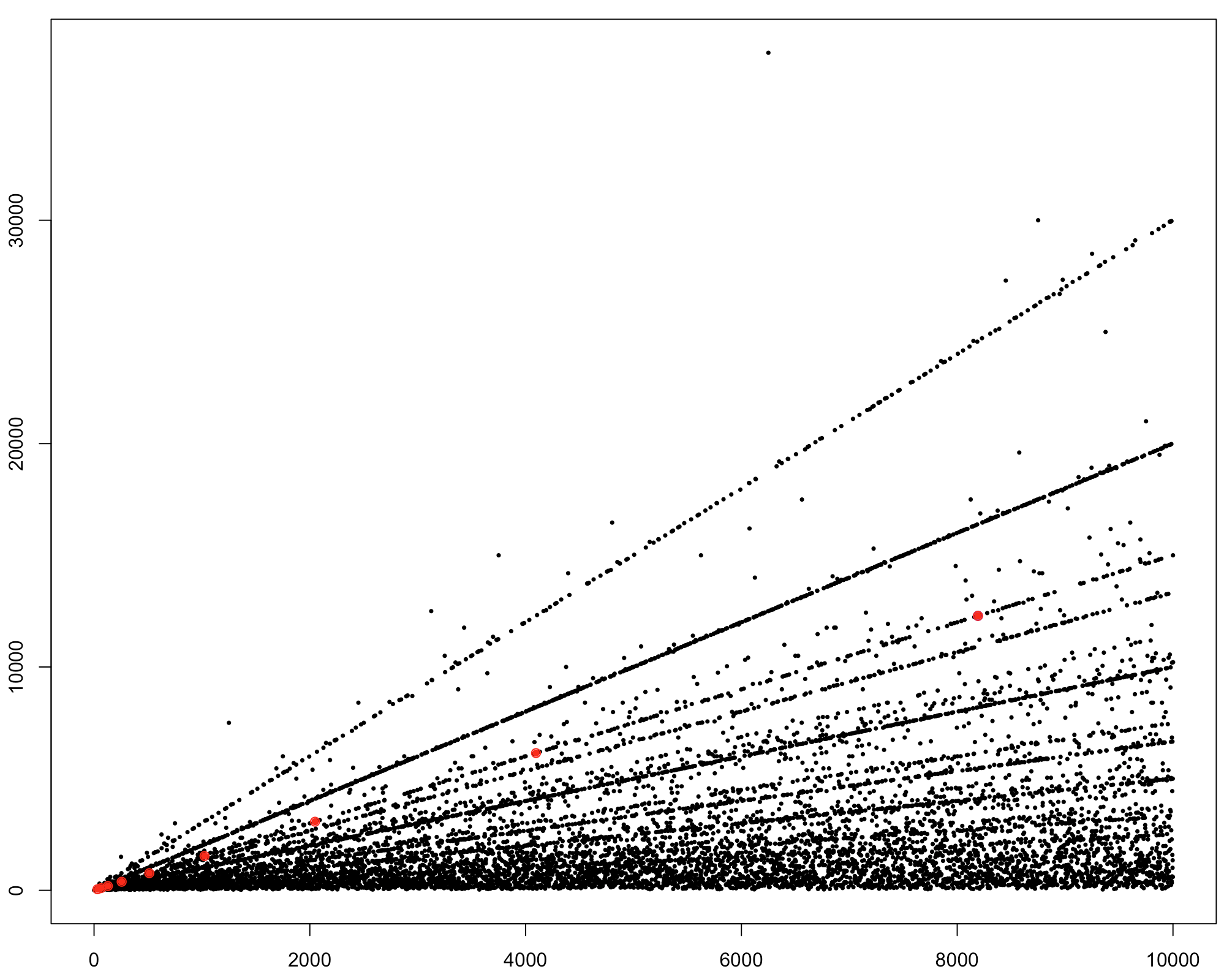
I have marked the points you are interested in in red. You see that there are way more points on that line.
-
Interesting.
So it turns out Fibonacci cycle lengths a thing people study. They’re called Pisano numbers and understanding them is really about understanding Pisano numbers for prime powers.
A neat property is that if n and m are coprime then period(mn) is least common multiple of period(n) and period(m).
