Puzzle time - the Triangle

[jon-nyc]

A teacher (lets call him Klaus) used to give this problem as part of his elementary geometry class:

A right triangle has hypotenuse (BC) of length 10, and a height (AP) of length 6. What is the area?

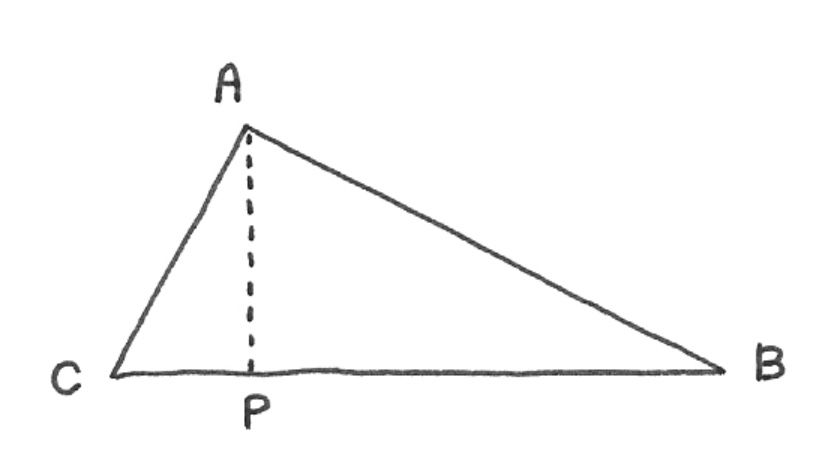
His average students (lets call them Horace and Ax) got full credit for the answer 1/2 * 10 * 6 = 30.

But a really smart kid (lets call her Taiwan girl) couldn’t solve the problem.

Why not?

[Axtremus]

:::

There are three hypothenuses. Which one has the length 10?

:::

[Klaus]

:::

Is it something as boring as "it isn't specified that AP is the height, so it could be something slightly different"?

:::

[jon-nyc]

@Axtremus BC has length 10

@Klaus AP is the height.

[Klaus]

Oh, now I see.

:::

AB isn't the hypotenuse.

:::

[jon-nyc]

Nope that was just a typo on my part when I went back to clarify!

[kluurs]

||AC represents the height - as the triangle is inverted for triangle CAB. 6 is the height of triangle PAB. ||

[Axtremus]

:::

I was trying to say that the “really smart” kid cannot solve the problem because of the ambiguity stemming from there having three possible right triangles in the diagram: ABC, ACP, ABP. So when you say something like the hypothenuse has length 10, it’s ambiguous whether you’re referring to which hypothenuse, AB, AC, or BC.

:::

[Nunatax]

:::

Too lazy to look up the required formulas right now, but with A fixed as a right angle and CB equal to 10, height AP will be confined to a certain range. I guess it's at its maximum when angles C and B are both 45 degrees and even then AP will likely be less than 6? If that's the case, the scenario is simply impossible.

:::

[jon-nyc]

I should have named the smart kid Nunatax.

The triangle is impossible as this simple diagram shows us:

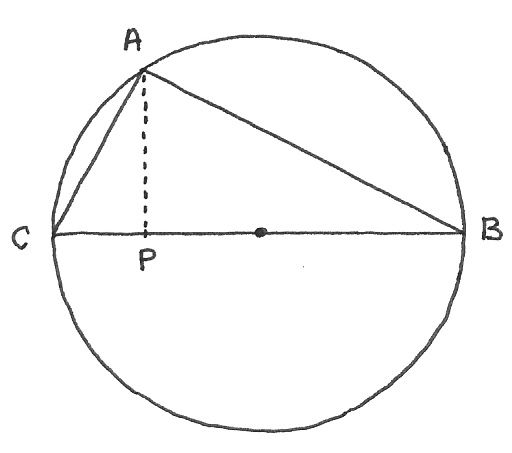
(Recall that, if the angle CAB is a right angle, it must lie on the perimeter of the circle, per Euclid

The maximum height of AP is 5.

[Klaus]

Nice!

I wonder what that restriction (of the maximal height) looks like in non-Euclidean geometries.

[Mik]

The original formula would only work if CAB was a right triangle anyway, or 1/2 a rectangle.

[taiwan_girl]

@jon-nyc said in Puzzle time - the Triangle:

I should have named the smart kid Nunatax.

Correct, you should not have picked me! 555