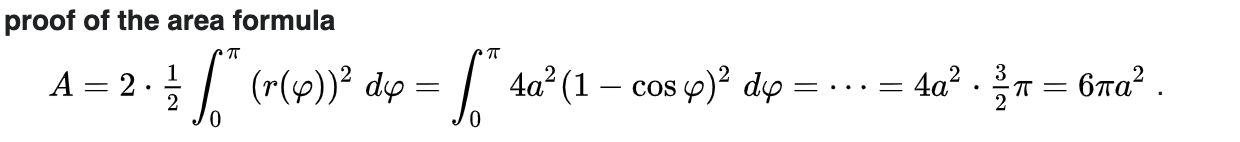Puzzle time - Silo dog

[Klaus]

silently meditating over the complexity of the formula for circle circle intersection

[jon-nyc]

Do keep in mind the perimeter traced out by the leash is not a circle, since the leash wraps around the silo when he goes behind it.

[Klaus]

Uh oh...

[jon-nyc]

This isn’t a ‘find the trick and do the answer in your head’ problem. It’s a pencil-to-paper problem.

[bachophile]

I figure the dog wanting to mark its territory simply pees all over the place.

[Klaus]

Game plan would be:

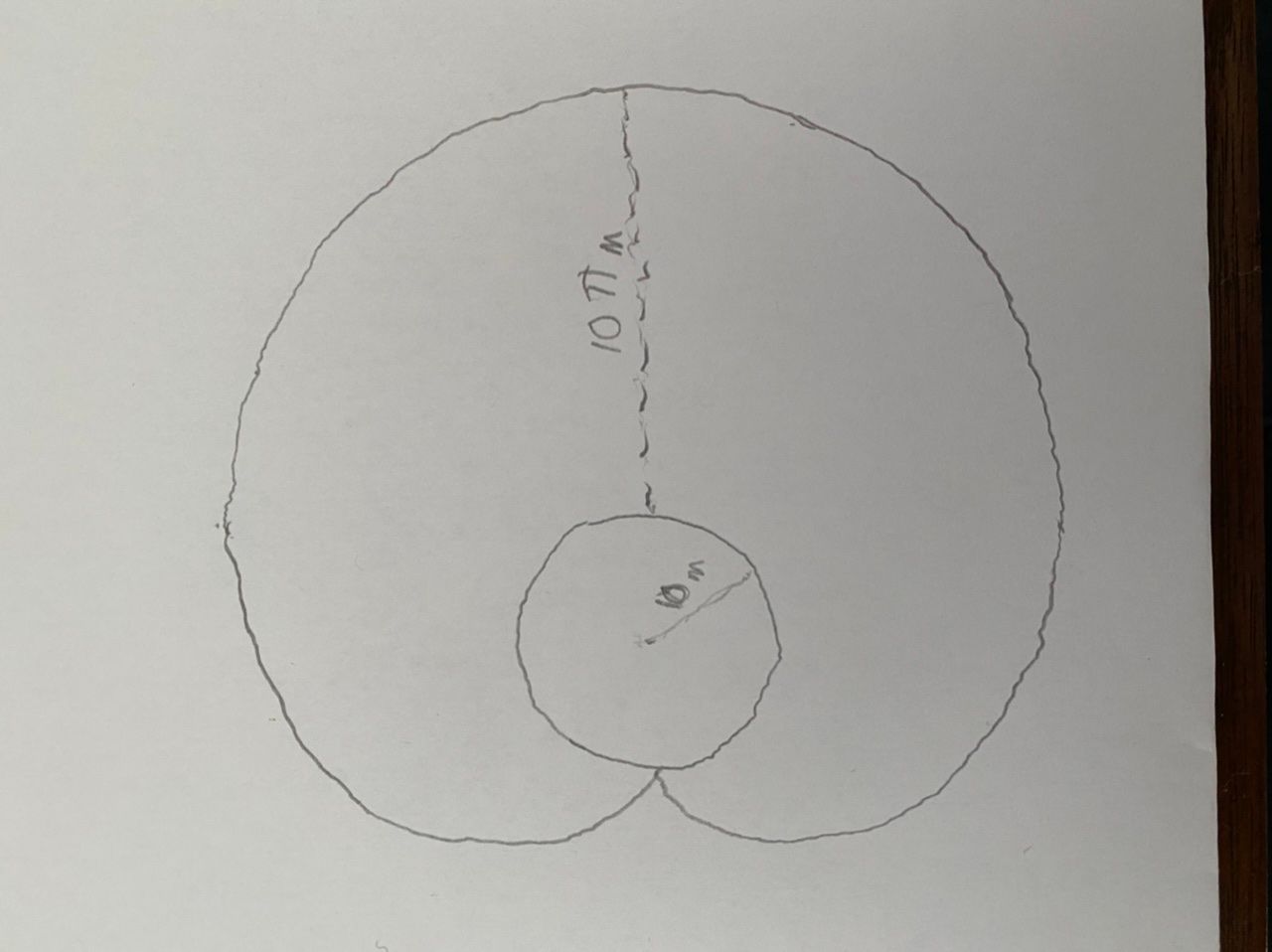
1. Find function that computes max height/distance from any point on silo, i.e., the shape of the "wrap around" part.

2. Presuming the formula is complicated, ask computer algebra system to integrate the function to find its area.

3. Multiply by two and add area of the semi-circle.

[Axtremus]

Yeah, getting the the “game plan” is easy, actually getting step 1 is the harder part.

[jon-nyc]

Actually integrating the function is straightforward.

The trick, if you want to call it that, is just figuring out the function. Totally doable by both of you.

[bachophile]

I glad he didn’t say the three of you

[jon-nyc]

lol.

[Axtremus]

||Cycloid is key.
Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid, and the area under the cycloid is given by the formula 3πr^2 where r is the silo's radius.
Solution is (area of cycloid traced out by the silo)-(area of silo)+(half the area of circle with radius that is the leash's length).
Area covered by the dog = 3π(10)^2 - π(10)^2 + (π(10π)^2)/2
||

[Klaus]

@Axtremus said in Puzzle time - Silo dog:

Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid,

But how does that arc relate to where the dog can go? Your solution - which may well be correct - is missing an argument here.

[Klaus]

Wouldn't the resulting shape be a (part of a) cardoid and not a cycloid?

[jon-nyc]

Yes. This is the shape. Note the 10pi leash length is just perfectly half the circumference of the silo.

[Axtremus]

Right, cardioid rather than cycloid.

[jon-nyc]

Maybe you can google up a formula if you can’t figure out the integral.

[Klaus]

I haven't looked at formulas yet but it looks like one needs only a part of the cardoid area since it overlaps with the semi circle.

[jon-nyc]

Yep. It’s the quarter circle plus that bit of cartioid x 2

[Klaus]

The area formula is:

but the integral would not have to be taken to pi but to the angle at which the y value is maximal, would be the case at the angle 3/4 * sqrt(3).

But this gets rather complicated hence I assume something's wrong here...

[jon-nyc]

That's ugly don't continue.

Smallish hint:

||Look at the cardioid area in isolation and write an equation for the length of the leash as a function of the angle traversed through it.||

Biggish hint:

||Imagine the dog is at the "northern" border between the half circle and the cardioid part as shown in this diagram:

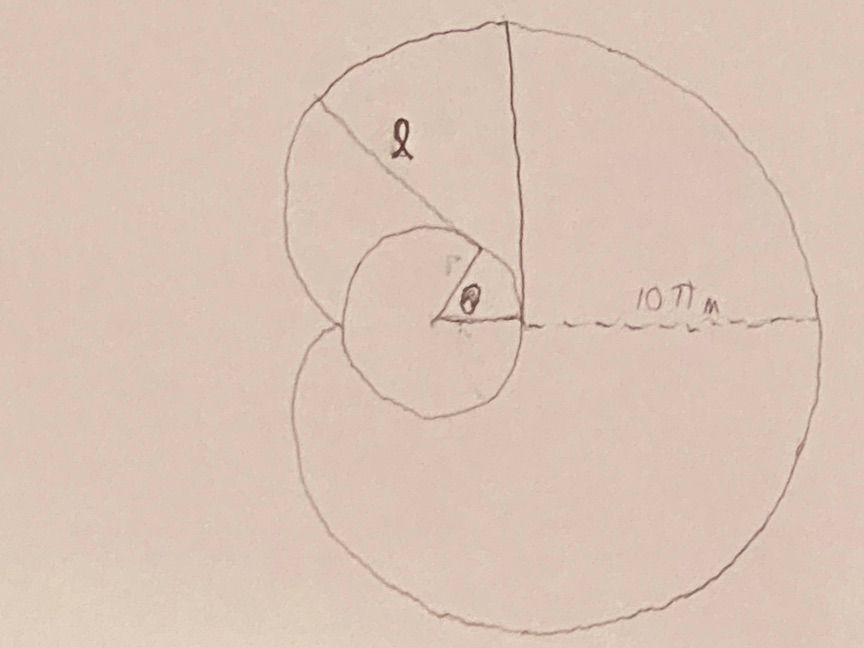
His leash is now a tangent on the circle formed by the silo.

As he moves "west" the leash shortens but continues drawing a tangent against the circle. As a first step, express the length 𝓁 of the leash as a function of the angle θ.||