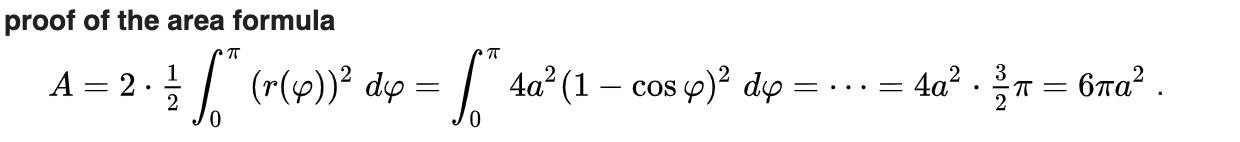Puzzle time - Silo dog
-
I figure the dog wanting to mark its territory simply pees all over the place.
-
Game plan would be:
-
Find function that computes max height/distance from any point on silo, i.e., the shape of the "wrap around" part.
-
Presuming the formula is complicated, ask computer algebra system to integrate the function to find its area.
-
Multiply by two and add area of the semi-circle.
-
-
I glad he didn’t say the three of you
-
||Cycloid is key.
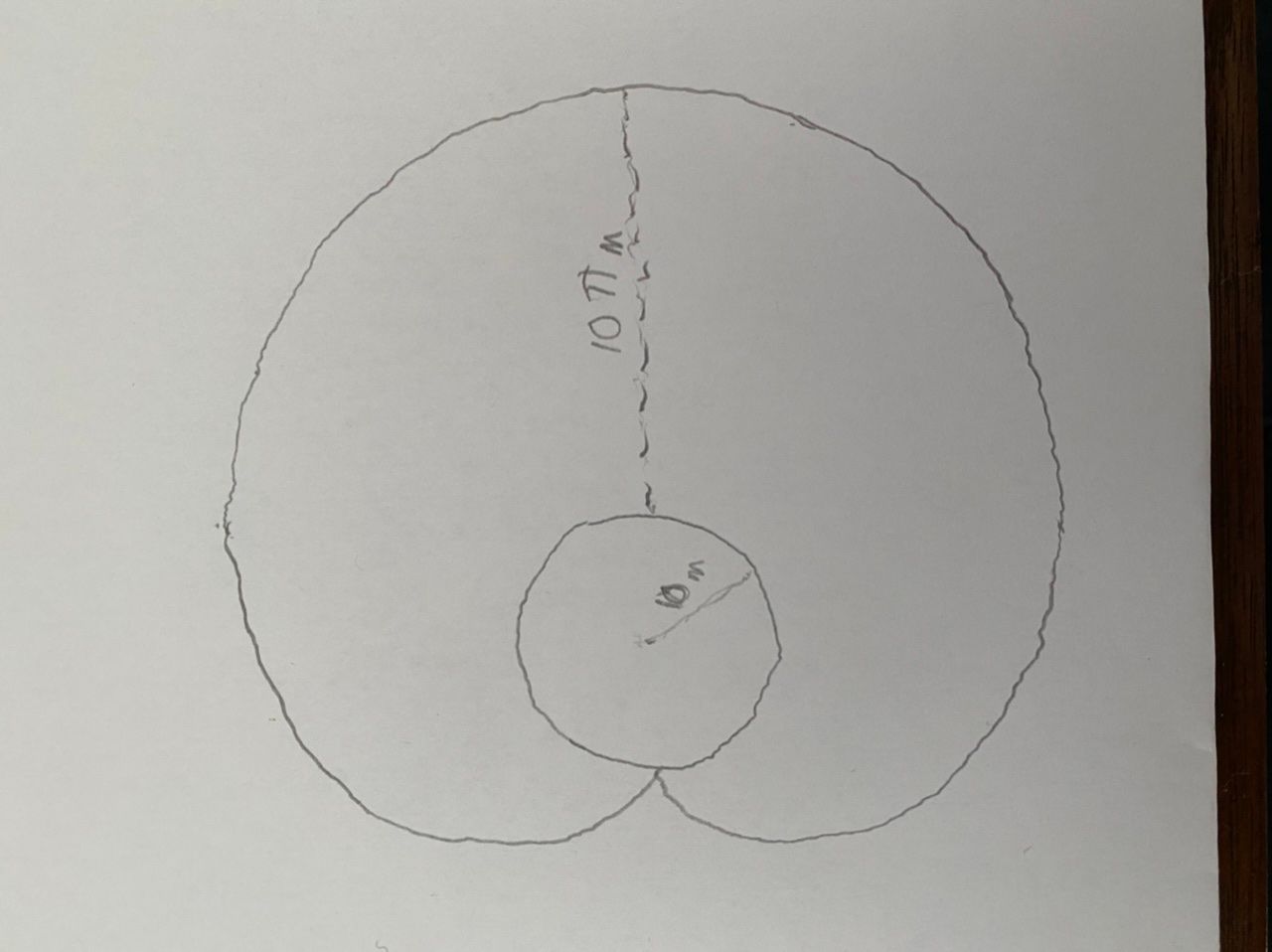
Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid, and the area under the cycloid is given by the formula 3πr^2 where r is the silo's radius.
Solution is (area of cycloid traced out by the silo)-(area of silo)+(half the area of circle with radius that is the leash's length).
Area covered by the dog = 3π(10)^2 - π(10)^2 + (π(10π)^2)/2
|| -
||Cycloid is key.
Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid, and the area under the cycloid is given by the formula 3πr^2 where r is the silo's radius.
Solution is (area of cycloid traced out by the silo)-(area of silo)+(half the area of circle with radius that is the leash's length).
Area covered by the dog = 3π(10)^2 - π(10)^2 + (π(10π)^2)/2
||@Axtremus said in Puzzle time - Silo dog:
Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid,
But how does that arc relate to where the dog can go? Your solution - which may well be correct - is missing an argument here.