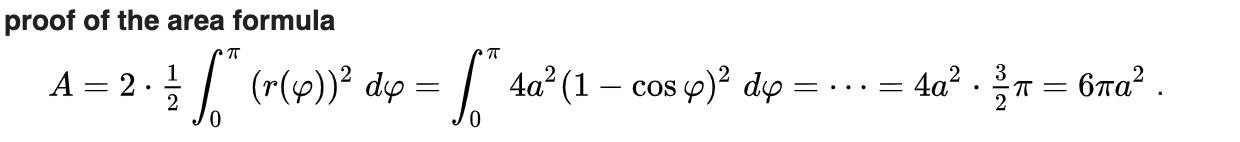Puzzle time - Silo dog
-
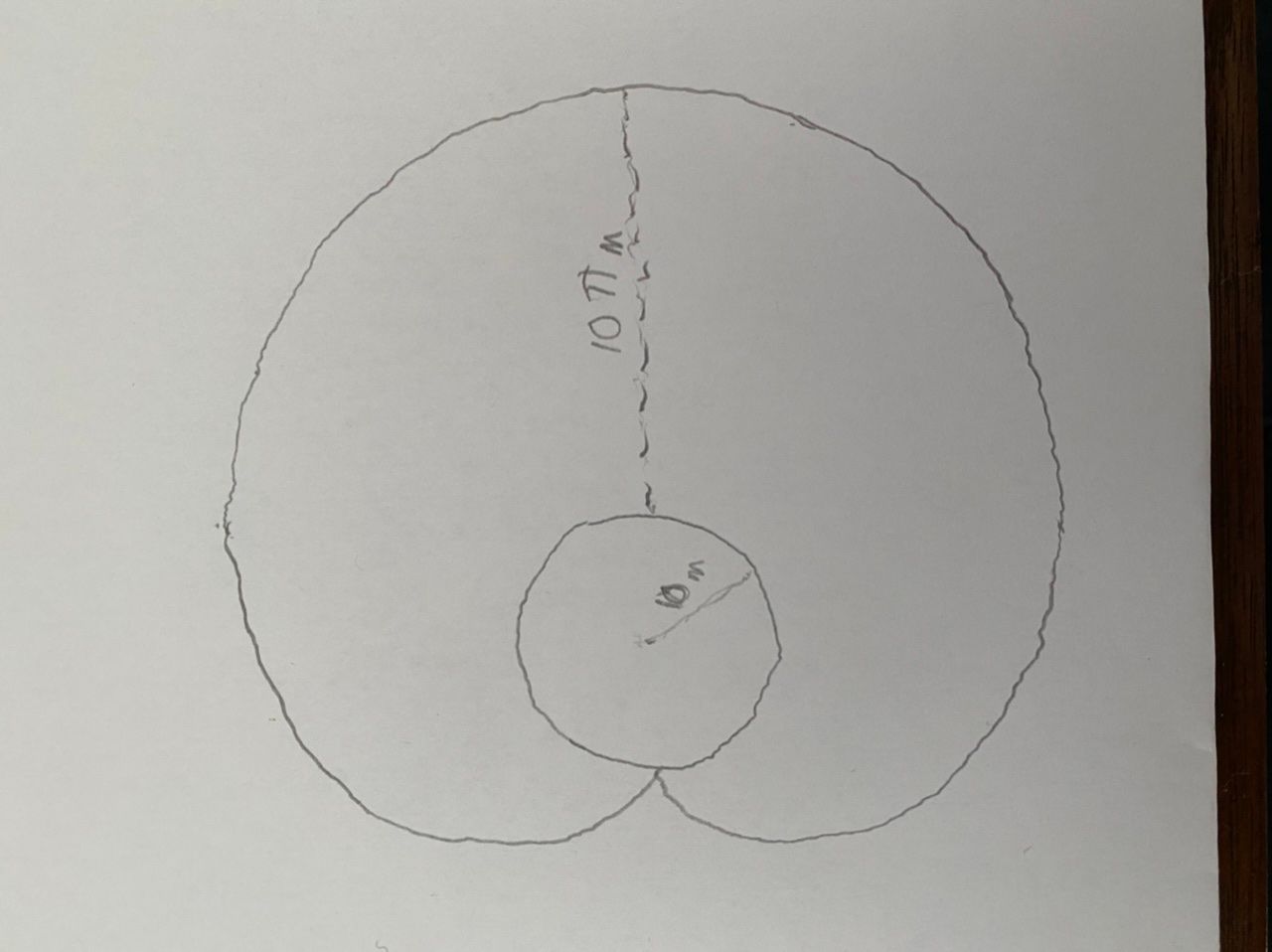
||Cycloid is key.
Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid, and the area under the cycloid is given by the formula 3πr^2 where r is the silo's radius.
Solution is (area of cycloid traced out by the silo)-(area of silo)+(half the area of circle with radius that is the leash's length).
Area covered by the dog = 3π(10)^2 - π(10)^2 + (π(10π)^2)/2
|| -
||Cycloid is key.
Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid, and the area under the cycloid is given by the formula 3πr^2 where r is the silo's radius.
Solution is (area of cycloid traced out by the silo)-(area of silo)+(half the area of circle with radius that is the leash's length).
Area covered by the dog = 3π(10)^2 - π(10)^2 + (π(10π)^2)/2
||@Axtremus said in Puzzle time - Silo dog:
Imagine the silo "rolls over" by 180º, the arc traced out by the point opposite the hook is that of a cycloid,
But how does that arc relate to where the dog can go? Your solution - which may well be correct - is missing an argument here.
-
That's ugly don't continue.
Smallish hint:
||Look at the cardioid area in isolation and write an equation for the length of the leash as a function of the angle traversed through it.||
Biggish hint:
||Imagine the dog is at the "northern" border between the half circle and the cardioid part as shown in this diagram:
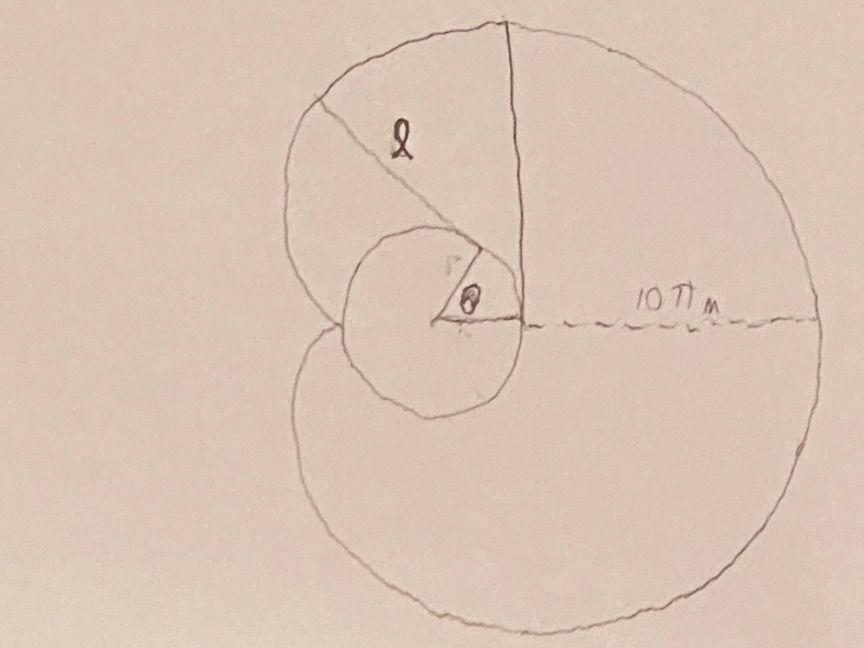
His leash is now a tangent on the circle formed by the silo.
As he moves "west" the leash shortens but continues drawing a tangent against the circle. As a first step, express the length 𝓁 of the leash as a function of the angle θ.||
-
Here it is, in a spoiler in case someone still wants to solve it.
||As previously noted, the total area comprises a half circle plus that little strange part which apparently is called a cardioid (a word I don't remember hearing before this thread.
The half circle is easy, 1/2(pi * r^2), where the radius is 10pi, so 50pi^3.
Now for the cardioid area. Note in the following diagram, when stretched taut the length of the remaining leash after it has already wrapped around a portion of the silo wall is the total length of the leash minus the circumference of the arc it has traversed. So if we call the angle t the length is 10pi - 10t, or 10(pi-t).
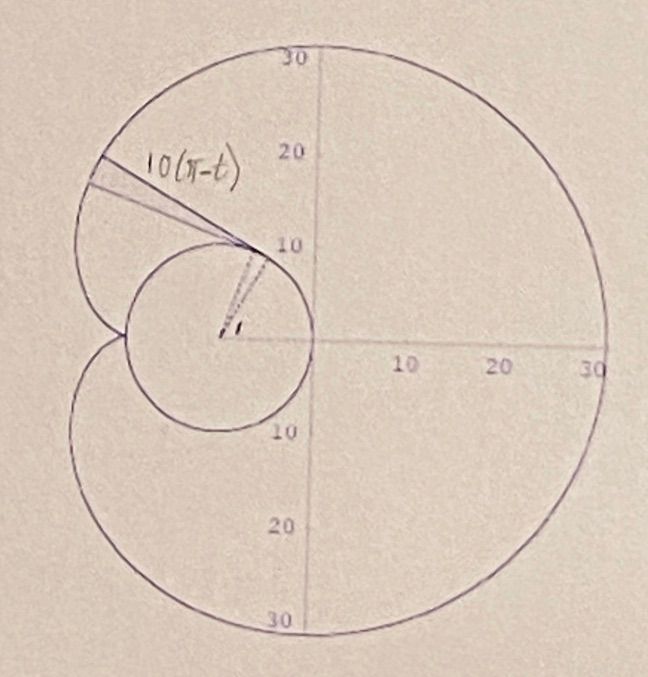
Now for a little calculus. Increase t by a tiny amount - dt. The tangent advances correspondingly, and the area of the tiny sector of the circle you've covered is 50(pi-t)^2 dt. Integrate that from 0 to pi and you get 50/3 * pi^3.
Double that to get 100/3 * pi^3 and add the half circle and the final answer is 250/3 * pi^3.||
-
Sorry, I was too lazy to continue.
Could you tell me where the 50(pi-t)^2 dt comes from?
Also, it is not obvious to me that the integral gives you the area. The ordinary (Riemann) integral computes the limit of the area of a sequence of boxes, like so:

But you are filling the area with sectors of circles. It's not obvious to me that the methods of Riemann integration work in that setting. I'm not saying it's wrong; I'm saying it's not obviously correct.
-
I'll answer the second question first. Though you're kind of saying "Hey Jon, can you derive polar calculus for me"? Which I probably never did but if so it was at age 17. SO here's my non-rigorous attempt.
It's very analogous to Reimann sums but instead of rectangles you use sectors of a circle.
Here's an image of a generalized curve that I wish to integrate:
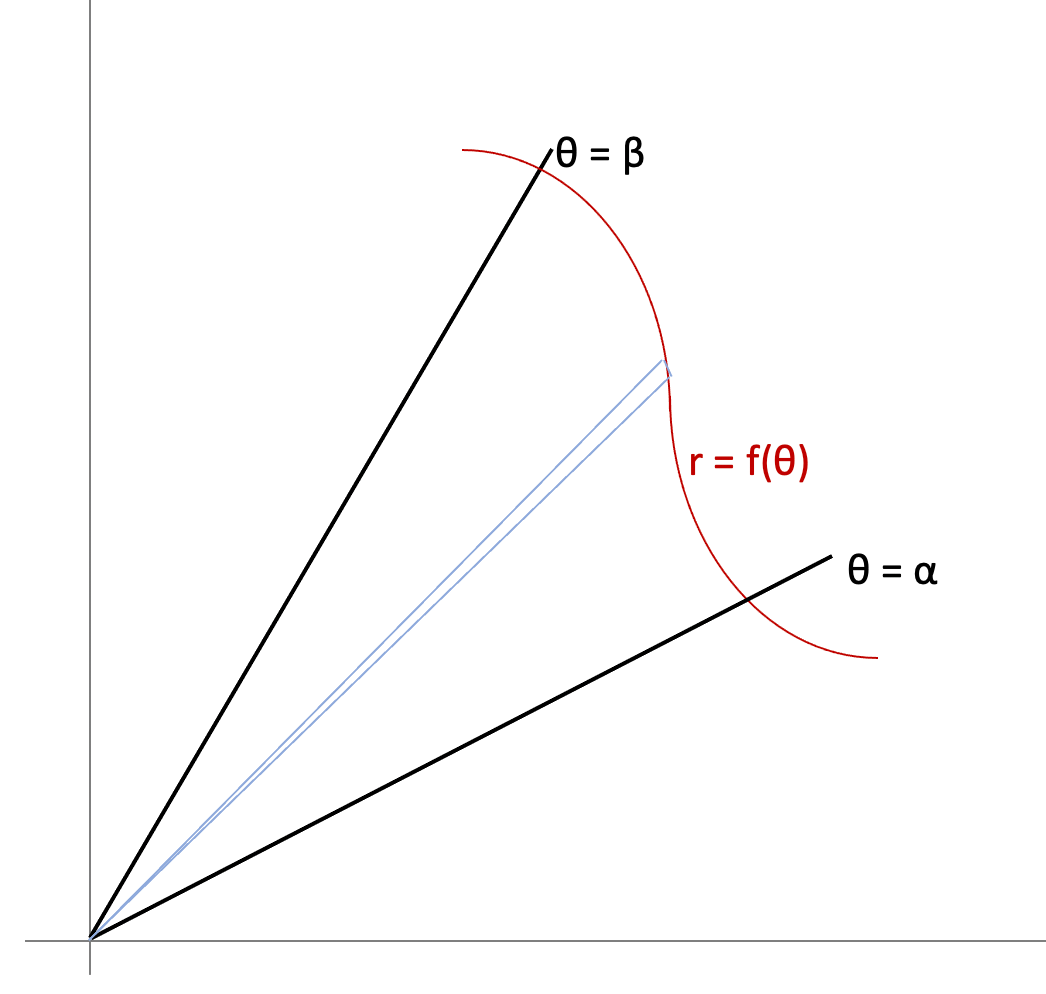
Say you want to find the area between the thick dark lines. Like with Reimann, you can approximate the area by dividing region between α and β into n sectors, compute the area of each, and sum them.
First, approximate the area in gray as a sector of a circle. For that you compute the area of the entire circle and multiply it by the ratio of the angle of that little sector to 2π.
Radius = f(θi), angle = Δ(θi)
A~= π r^2 * Δ(θi)/2π = ½ f(θi)^2 Δ(θi)Now sum them up: (forgive my notation, I can’t do both sub and superscript in front of the sigma sign)
Σ(i=1 to i=n) ½ f(θi)^2 Δ(θi)
Take limit n-> infinity and you get : (again the notation problem)
½ ∫(α to β) f(θ)^2 dθ.
Now for the second question. It's not the most straightforward application of the above, since it is an area between two curves. But you can easily see that the area can be also be approximated by dividing it into a large number of sectors and summing the areas of each sector. Also it follows that as I increase n to infinity (IOW take the integral) the error of my approximation goes to zero.
In this case is the 'radius' of each individual sector is 10(π-θ). The area of each sector is:
½ f(θi)^2 Δ(θi),
½ * (10(π-θ))^2 * dθ
or 50 * (π-θ) ^2 * dθ
-
Giving it thought this morning, I’ll bet the generalized method of Riemann integrals would work with just about any method of subdividing the area of interest into non-overlapping sub-areas, as long as the limit of the error approached 0 as n approached infinity.
You could fill an area with n circles for example. It would just lead to obscene calculations.
Think of this analogy from real life: you have a large fish tank. First approximate its volume by seeing how many apples it will hold. Then try golf balls. Then marbles. Then BBs. Then grains of sand. Then water molecules.
-
Jon, obviously you can fill the area with all kinds of shapes, be it rectangles, or circle sectors, or whatnot, and the limit of the construction will give you the area. That's not my point.
The point is whether the properties of that construction are the same as for the Riemann integral.
For instance, the Riemann integral is a linear transformation: The integral of af(x)+bg(x) is the same as a*(integral of f(x)) + b*(integral of g(x)). The linearity is what we use in the normal calculus rules for polynomials, for instance. From what I can see, you used those polynomial integration rules on your function, and it was (and still isn't) obvious to me that it is sound to use those rules in your setting.
-
Area integrals of polar curves seems to be a thing.
https://brilliant.org/wiki/polar-curves/#area-integrals-of-polar-curvesLooks like you had the right intuition.
I think the formal answer why this works is that the sum of the circle arcs can be reinterpreted as a sum of rectangles, i.e., a Riemann sum, so implicitly all the circle arcs are transformed into rectangles of the same area.