Puzzle time - making a triangle

[jon-nyc]

A perfectly thin straight rod receives two marks placed at random (uniform distribution).

If you break the rod at those two points, what are the odds you could form a triangle with the pieces?

[Klaus]

Can you rearrange the pieces or do you have to use them in the order they were in when they were part of the rod?

[Klaus]

My first thought when thinking about this: triangle inequality.

[Horace]

It boils down to whether the shortest two pieces sum to a length greater than the largest piece.

[Klaus]

:::

25%

:::

[Axtremus]

@horace said in Puzzle time - making a triangle:

It boils down to whether the shortest two pieces sum to a length greater than the largest piece.

:::

I found a way to cheat (as in I’m pretty sure this is not what @jon-nyc has in mind): you can always form a triangle as long as you do not mind parts of the rods “sticking outside” the triangle.

:::

[Klaus]

I think I found a nice way to illustrate the solution of the problem in one word that doesn't give away anything:

Butterfly.

[jon-nyc]

@Klaus

Show your work.

[Klaus]

@jon-nyc Does the word "Butterfly" not convince you that I did my homework?

[Klaus]

:::

This is my butterfly.

Obviously it occupies 25% of the square.

:::

[jon-nyc]

Give your quick reasoning? Funny, I’ve thought of two other ways to solve it.

[Klaus]

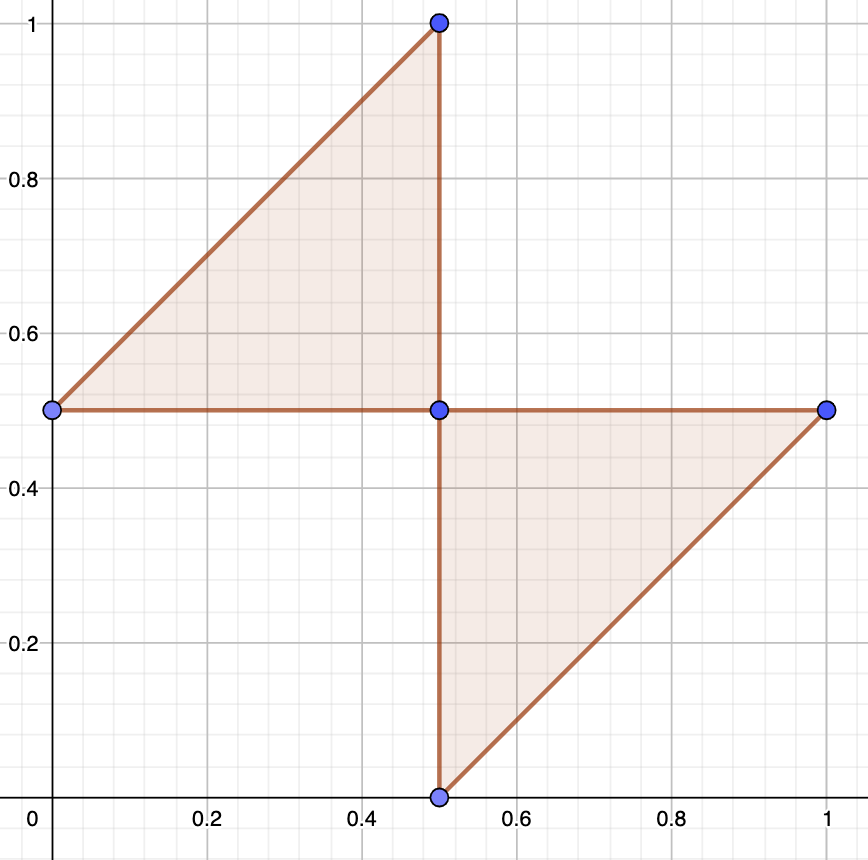
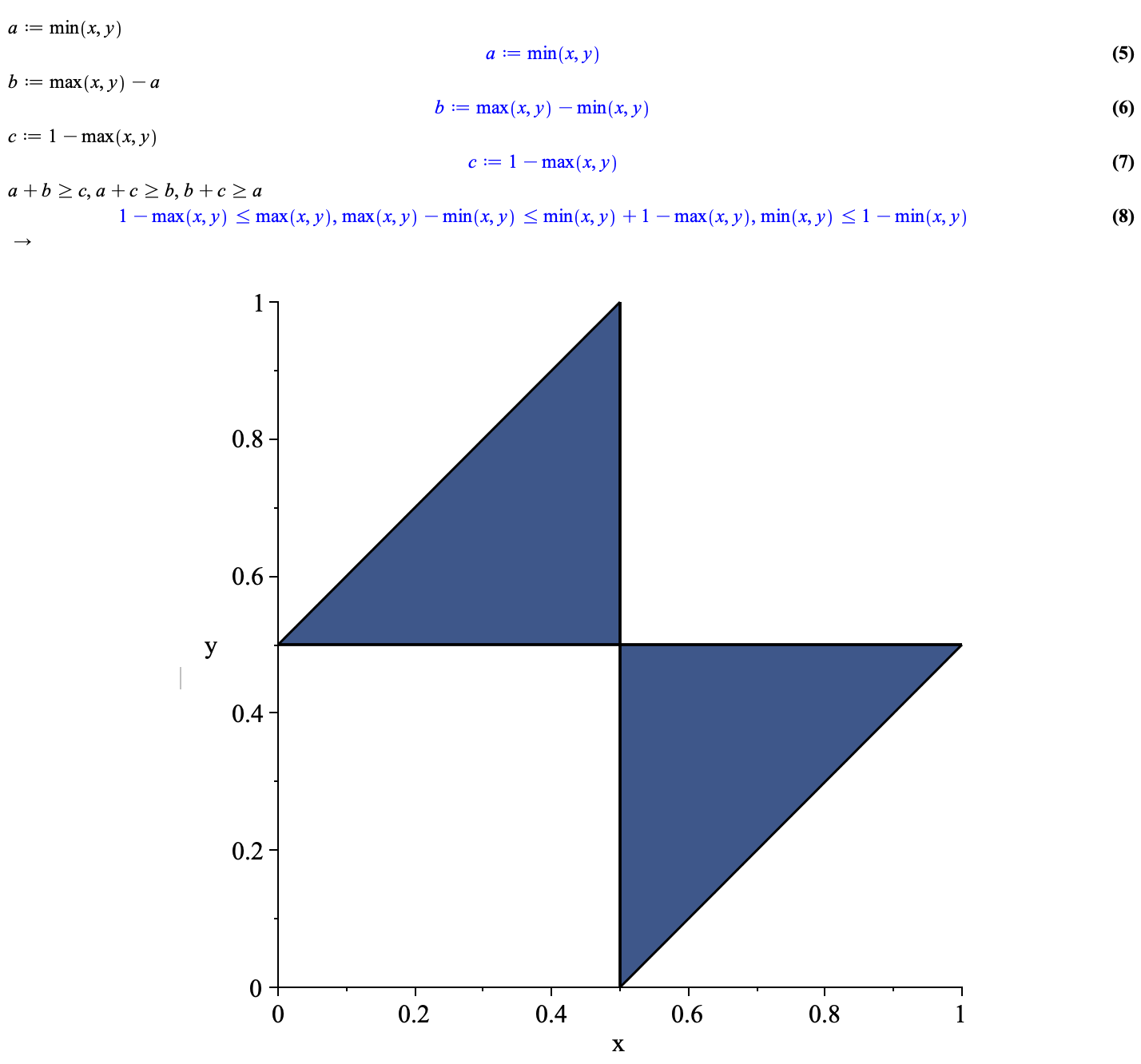
Well, the x and y axis of my graph denote the randomly drawn numbers. The butterfly denotes the pairs of random numbers that result in pieces that satisfy the triangle inequality.

It’s the graph of the inequalities a+b >=c, a+c>= b, b+c >= a where a = min(x,y), b = max(x,y)-min(x,y) and c = 1-max(x,y). That is, a,b,c are the lengths of the pieces given cuts at x and y.

I guessed that this would be the obvious way to solve it hence my guess that you’d “get” the butterfly reference. Now I’m curious about your solution.

[jon-nyc]

I did get it, was just thinking about others that might see it.

:::
The official solution is like yours but in three dimensions. Consider x, y, and z the length of the three segments.

You need to satisfy the equations:

x+y+z=1
x+y>z
x+z>y
y+z>x
(with x,y, and x only being between 0 and 1)

Put them on a unit cube in 3d cartesian coordinates. You see all the triplets satisfying the first equation is a diagonal plane that slices off a corner of this cube, and the values between 0 and 1 lie in an equilateral triangle on this plane with vertices (0,0,1) (0,1,0) (1,0,0). (That's the universe of probabilities that is equivalent to the square from which your butterfly is cut).

To apply the inequalities, just see where the three planes (x+y-z=0), (x+z-y=0), (y+z-x=0) intersect with our plane. You find they go from midpoint to midpoint of its sides, cutting our equilateral triangle into four smaller identical ones. The region satisfying the inequalities is the innermost triangle, thus 1/4.

Now here's an easier method:

Picture the rod as a circle, with the first point being the two ends of the rod.

Now the exercise is choosing two points at random, and the test is that there can't be an arc of pi radians between any two points.

Anchor the first point at 0, and the second point at theta <=pi (WOLOG). Then the third point must be between pi and pi+theta.

So the probability is the expected vale of theta/2pi as theta ranges from 0 to pi: 1/4
:::

[Mik]

[Klaus]

@jon-nyc said in Puzzle time - making a triangle:

Picture the rod as a circle

Looks like a conceptual move, not an algebraic one.

Link to video

Eh, time stamps don't seem to work in embedded videos. Forward to 3:25.

[Klaus]

I thought this might be a good excuse to toy around with Maple a little, which I have wanted to do for a while.

Works nicely.