Puzzle time - making a triangle
-
It boils down to whether the shortest two pieces sum to a length greater than the largest piece.
@horace said in Puzzle time - making a triangle:
It boils down to whether the shortest two pieces sum to a length greater than the largest piece.
:::
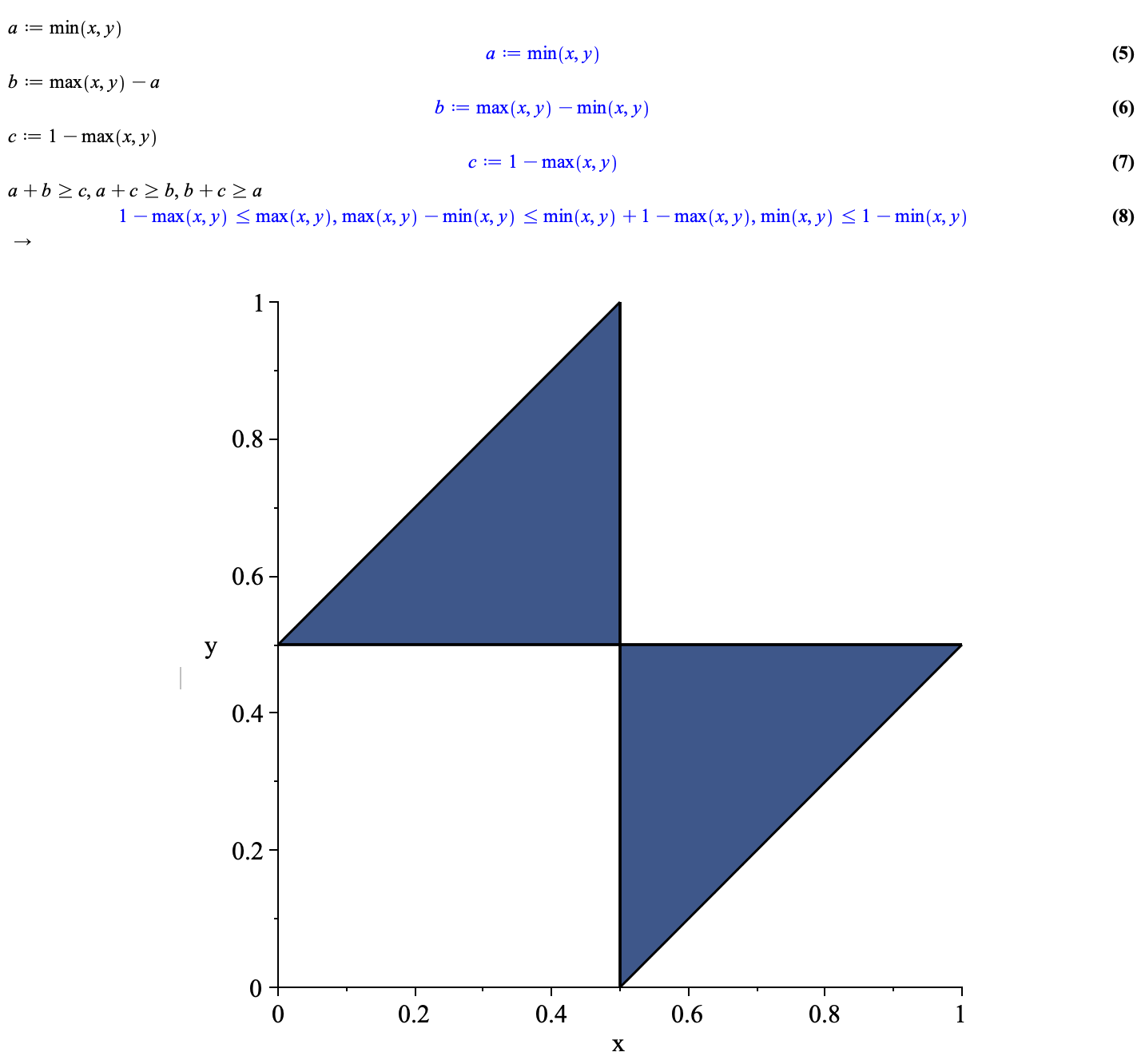
I found a way to cheat (as in I’m pretty sure this is not what @jon-nyc has in mind): you can always form a triangle as long as you do not mind parts of the rods “sticking outside” the triangle.
:::
-
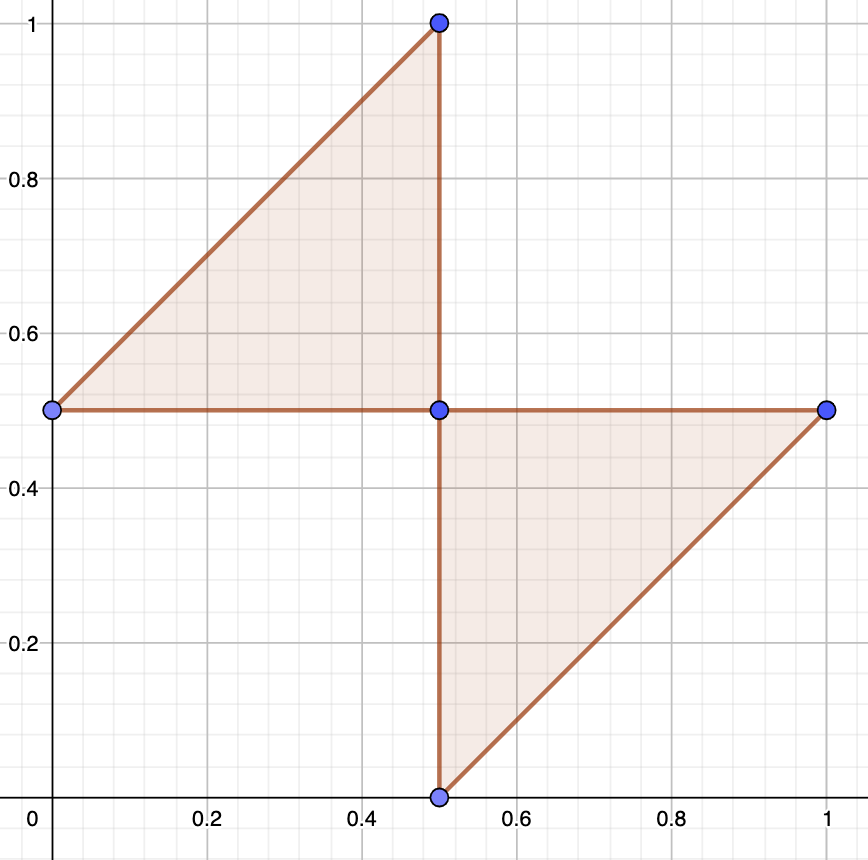
Well, the x and y axis of my graph denote the randomly drawn numbers. The butterfly denotes the pairs of random numbers that result in pieces that satisfy the triangle inequality.
It’s the graph of the inequalities a+b >=c, a+c>= b, b+c >= a where a = min(x,y), b = max(x,y)-min(x,y) and c = 1-max(x,y). That is, a,b,c are the lengths of the pieces given cuts at x and y.
I guessed that this would be the obvious way to solve it hence my guess that you’d “get” the butterfly reference. Now I’m curious about your solution.
-
I did get it, was just thinking about others that might see it.
:::
The official solution is like yours but in three dimensions. Consider x, y, and z the length of the three segments.You need to satisfy the equations:
x+y+z=1
x+y>z
x+z>y
y+z>x
(with x,y, and x only being between 0 and 1)Put them on a unit cube in 3d cartesian coordinates. You see all the triplets satisfying the first equation is a diagonal plane that slices off a corner of this cube, and the values between 0 and 1 lie in an equilateral triangle on this plane with vertices (0,0,1) (0,1,0) (1,0,0). (That's the universe of probabilities that is equivalent to the square from which your butterfly is cut).
To apply the inequalities, just see where the three planes (x+y-z=0), (x+z-y=0), (y+z-x=0) intersect with our plane. You find they go from midpoint to midpoint of its sides, cutting our equilateral triangle into four smaller identical ones. The region satisfying the inequalities is the innermost triangle, thus 1/4.
Now here's an easier method:
Picture the rod as a circle, with the first point being the two ends of the rod.
Now the exercise is choosing two points at random, and the test is that there can't be an arc of pi radians between any two points.
Anchor the first point at 0, and the second point at theta <=pi (WOLOG). Then the third point must be between pi and pi+theta.
So the probability is the expected vale of theta/2pi as theta ranges from 0 to pi: 1/4
:::"You never know what worse luck your bad luck has saved you from."
-Cormac McCarthy -
I did get it, was just thinking about others that might see it.
:::
The official solution is like yours but in three dimensions. Consider x, y, and z the length of the three segments.You need to satisfy the equations:
x+y+z=1
x+y>z
x+z>y
y+z>x
(with x,y, and x only being between 0 and 1)Put them on a unit cube in 3d cartesian coordinates. You see all the triplets satisfying the first equation is a diagonal plane that slices off a corner of this cube, and the values between 0 and 1 lie in an equilateral triangle on this plane with vertices (0,0,1) (0,1,0) (1,0,0). (That's the universe of probabilities that is equivalent to the square from which your butterfly is cut).
To apply the inequalities, just see where the three planes (x+y-z=0), (x+z-y=0), (y+z-x=0) intersect with our plane. You find they go from midpoint to midpoint of its sides, cutting our equilateral triangle into four smaller identical ones. The region satisfying the inequalities is the innermost triangle, thus 1/4.
Now here's an easier method:
Picture the rod as a circle, with the first point being the two ends of the rod.
Now the exercise is choosing two points at random, and the test is that there can't be an arc of pi radians between any two points.
Anchor the first point at 0, and the second point at theta <=pi (WOLOG). Then the third point must be between pi and pi+theta.
So the probability is the expected vale of theta/2pi as theta ranges from 0 to pi: 1/4
:::@jon-nyc said in Puzzle time - making a triangle:
Picture the rod as a circle
Looks like a conceptual move, not an algebraic one.
Link to videoEh, time stamps don't seem to work in embedded videos. Forward to 3:25.
