Geometry problems ...

[Klaus]

Here's the same method for task B. Solution is X=8.43

[jon-nyc]

I got 8 and 9 also. Work shown in a minute

[Catseye3]

To one for whom math was the all-time bane, the three most hated words in school were "show your work".

[jon-nyc]

[Klaus]

Jon, I think you make an invalid assumption. Why do you assume that that other line you draw there has length 4 (or 3)?

[Horace]

The issue is that the length 5 drawn line is not necessarily parallel with the length x line.

[jon-nyc]

I almost posted that I was making that assumption, which may not be valid given the warning on the diagram.

[Klaus]

From my geometric method one can also derive an analytic solution. The formula is a little complicated, but the exact solution for X in the second problem is square root of 71, or 8.426149773176359.

Now I'm curious what Ax came up with.

[89th]

I feel dumb reading this thread. Most math (sorry, Maths, for Phibes) concepts have long since left my brain.

[Horace]

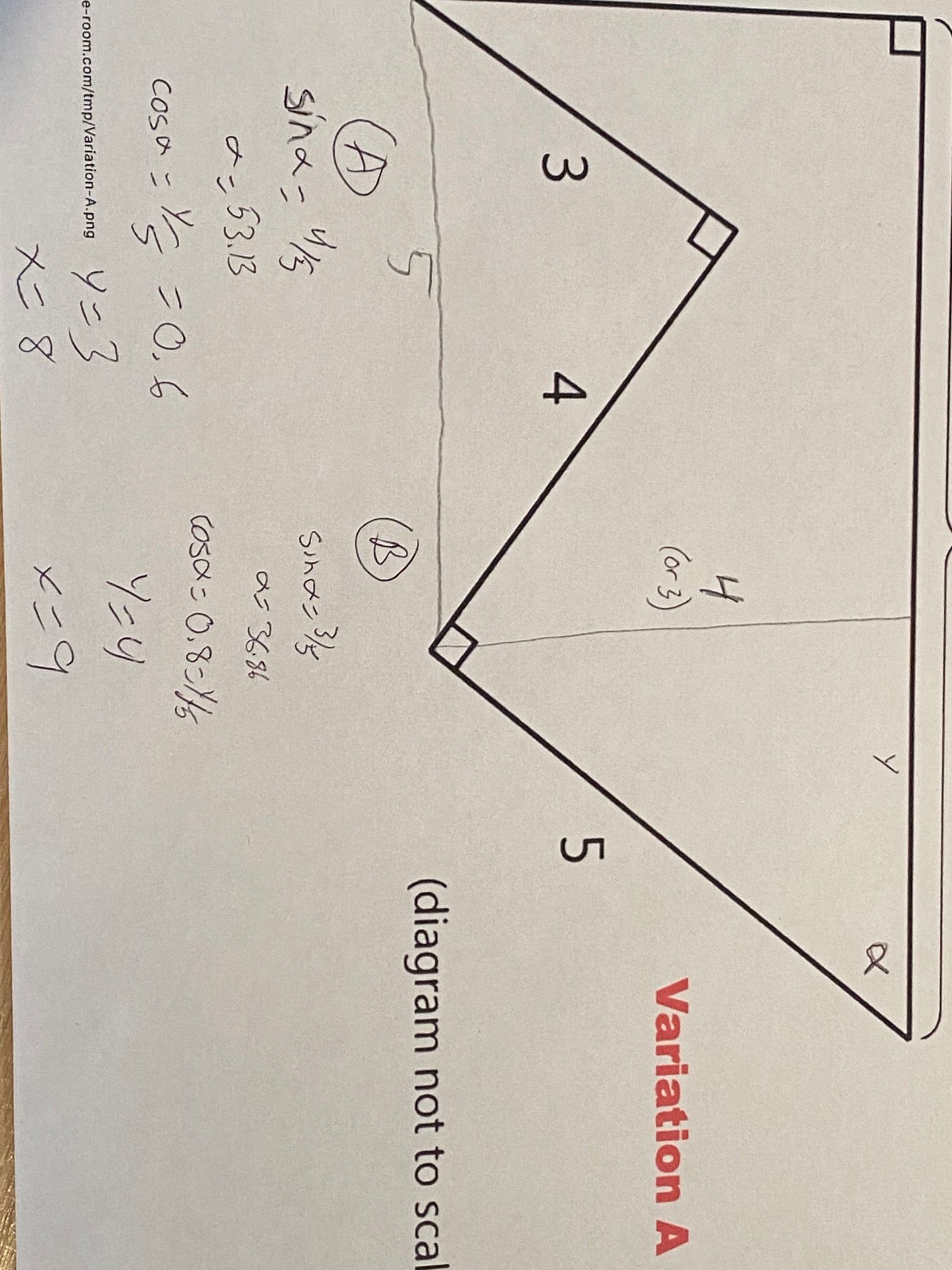
well the length of the line from the bottom left vertex to the top right vertex can be computed directly as the hypotenuse of a right triangle with the other two sides of length 8 and 4. That length gives you two lengths of a right triangle - 4 and that length in A, or 3 and that length in B. The third length is x. it's then an algebra problem using pythagoras. That method should work for both problems. Not elegant but not too complicated.

[Klaus]

@Horace said in Geometry problems ...:

well the length of the line from the bottom left vertex to the top right vertex can be computed directly as the hypotenuse of a right triangle with the other two sides of length 8 and 4.

I don't think so. Why should the length of the other side be 8?

[Horace]

I'm sliding the length 4 segment (the one in the middle) down the length 5 segment by 3 units so the length 4 segment touches the left vertical. That gives a right triangle of side lengths 4, 8, and sqrt(80). sqrt(80) is the hypotenuse of the right triangle with other lengths y and x, where y is either 3 or 4 in the two problems and x is the answer.

[Klaus]

Now I understand. Yes, that seems to work! That's actually the analytic solution that corresponds to my geometric solution.

[Horace]

Ax's method for problem A probably starts with the 8/4 right triangle idea and from there finds that x must be 8 because there are then two symmetric right triangles with their hypotenuses, er hypoteni, in common, and we know both have equal lengths of 4 for the short side and they must also have equal length for the long non-hypotenuse side, which in that case is 8, by the original idea of constructing the 8/4 triangle.

[Axtremus]

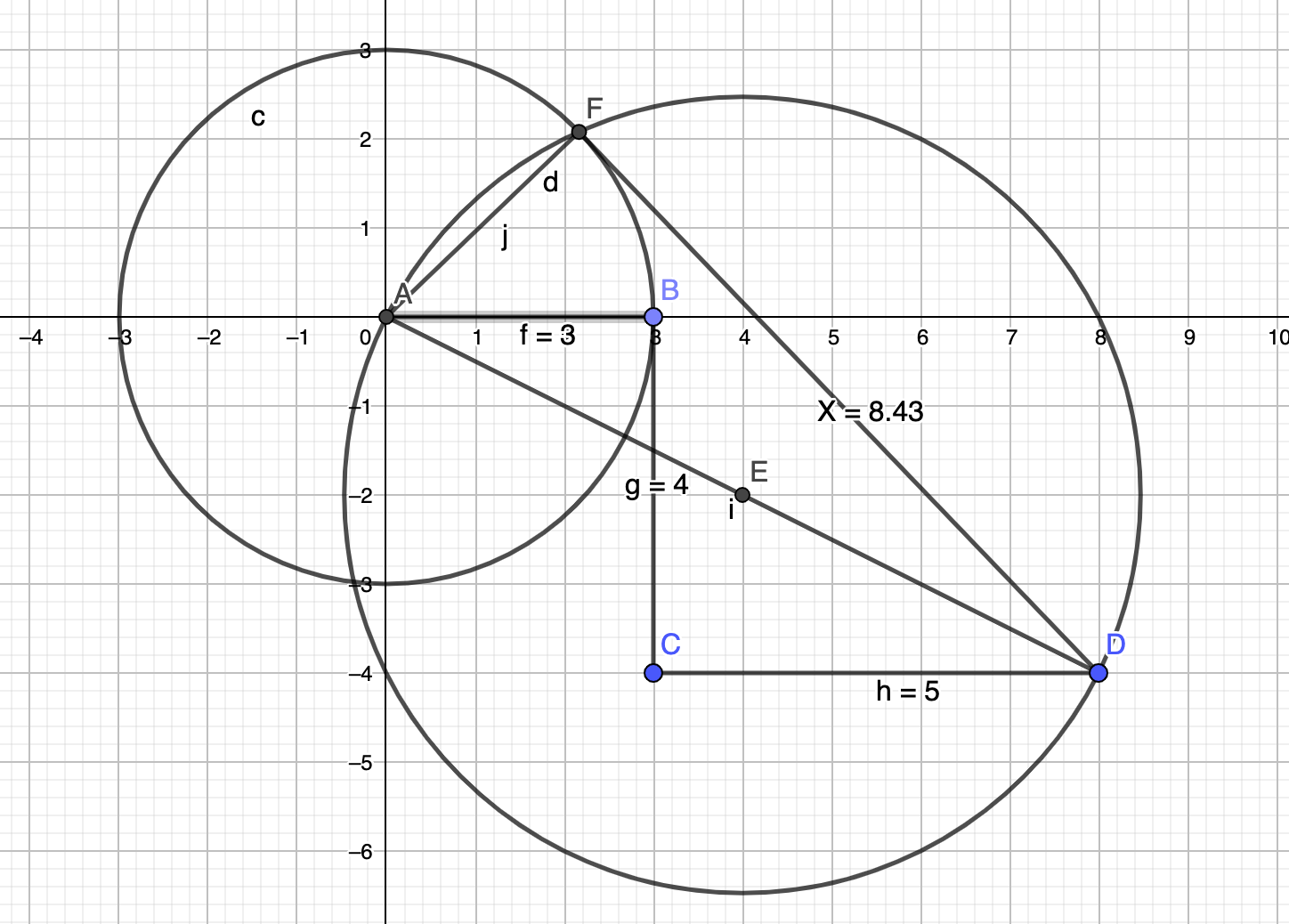
My solution to Variation-A:

The black outline polygon ABCDE is the information provided in the problem.

• Use the information from the BCDE line segments to construct the BF(D)E triangle.
• Realize that the BAE triangle is congruent to the BFE triangle.
• Hence the length of FE equals the length of AE, x = 8

[Axtremus]

My solution for Variation-B, as mentioned before, need to apply the Pythagorean Theorem twice, but it is essentially the same as already described by @Horace (4 posts above, and 6 posts above).

Some one made YouTube video that very nicely illustrated that solution:

Link to video

I got these two problems from that YouTube video.

[Horace]

In fairness, I also anticipated what your solution to variation A was, in my last post.

[Klaus]

That was a nice puzzle. Initially I made it way more complicated than it needed to be. I'm a little proud I found a solution that doesn't require Pythagoras or, for that matter, any formula at all