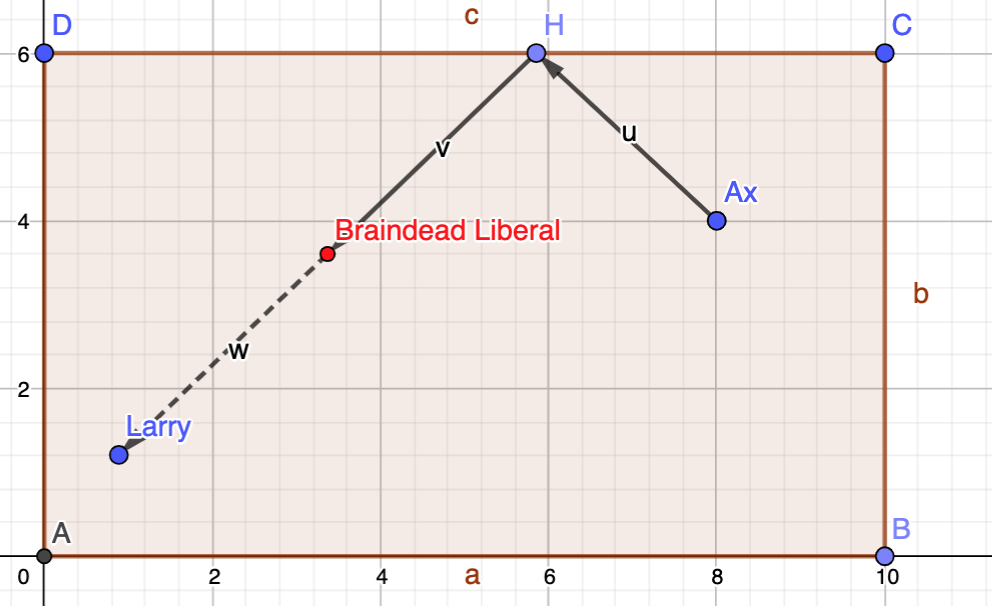
Puzzle time - don't waste braindead liberals

[jon-nyc]

That wasn’t correct. I need to fix it and repost.

[Klaus]

You are close. Many right ideas in your draft.

[jon-nyc]

I know it’s the second example I drew out which I didn’t like.

[jon-nyc]

I am confident my answer is right, just trying to show it’s exhaustive

[Klaus]

I think it's not exhaustive. You get only 11 distinct BDLs that way, not 16.

[jon-nyc]

I got 16. 25 possible segments, 9 fell out as redundant.

[Klaus]

9 are obviously redundant. But there are 4 more that are redundant. Do you want me to illustrate that?

[jon-nyc]

Not yet

[jon-nyc]

Yes so the midpoints, shifted if necessary, of the following segments:

A0-L0
A0-L1
A0-L2
A0-L3
A0-L4
A1-L2
A1-L3
A1-L4
A2-L3
A2-L4
A3-L4

Where A0 and L0 are the positions of Ax and Larry respectively. and A1-4 and L1-4 are their apparent positions in the 4 mirrors that surround them.

[Klaus]

Exactly. The detail that you presumably missed previously was that the situation is symmetric: The midpoint of A1-L2 is the same as A2-L1. That's why only 11 remain.

But those 11 aren't enough.

[jon-nyc]

I could put the arena on a coordinate system and define all the points of the 11 barriers in terms of Ax's coordinates x1,y1; Larry's coordinates x2,y2; and the width W and height(depth) H of the arena.

[jon-nyc]

That's what I was getting at earlier, wondering if they were exhaustive. I didn't look for higher-order reflections, assuming or hoping they'd collapse to the ones I'd defined. Give me some more time.

[Klaus]

If you want some data to play around with: I wrote down 10 lines of code to help me verify my method, which also supports your approach without many modifications (which shows that you are not far off from mine).

For instance, for this setup:

larry = (1.0,2.0)
ax = (8.0,5.0)
width = 10.0
height = 6.0

your approach yields the following 25 midpoints:

[(4.5,3.5),(4.5,7.5),(4.5,1.5),(13.5,3.5),(3.5,3.5),(4.5,4.5),(4.5,8.5),(4.5,2.5),(13.5,4.5),(3.5,4.5),(4.5,-1.5),(4.5,2.5),(4.5,-3.5),(13.5,-1.5),(3.5,-1.5),(6.5,3.5),(6.5,7.5),(6.5,1.5),(15.5,3.5),(5.5,3.5),(-3.5,3.5),(-3.5,7.5),(-3.5,1.5),(5.5,3.5),(-4.5,3.5)]

which, when shifted back, yield these 11 coordinates for BDLs:

[(3.5,1.5),(3.5,3.5),(3.5,4.5),(4.5,1.5),(4.5,2.5),(4.5,3.5),(4.5,4.5),(5.5,3.5),(6.5,1.5),(6.5,3.5),(6.5,4.5)]

[jon-nyc]

I think I got it. I need to add two additional reflections for each of Ax and Larry which amount to the double reflections off the pair of mirrors at each corner.

That gives me 36 segments, of which 20 drop out as redundant.

[jon-nyc]

This sketch shows the reflections for two arbitrary points.

[Klaus]

I agree with the 16, but why is that exhaustive?

[jon-nyc]

Proof tomorrow.

[Klaus]

OK, so this is what I got.

||

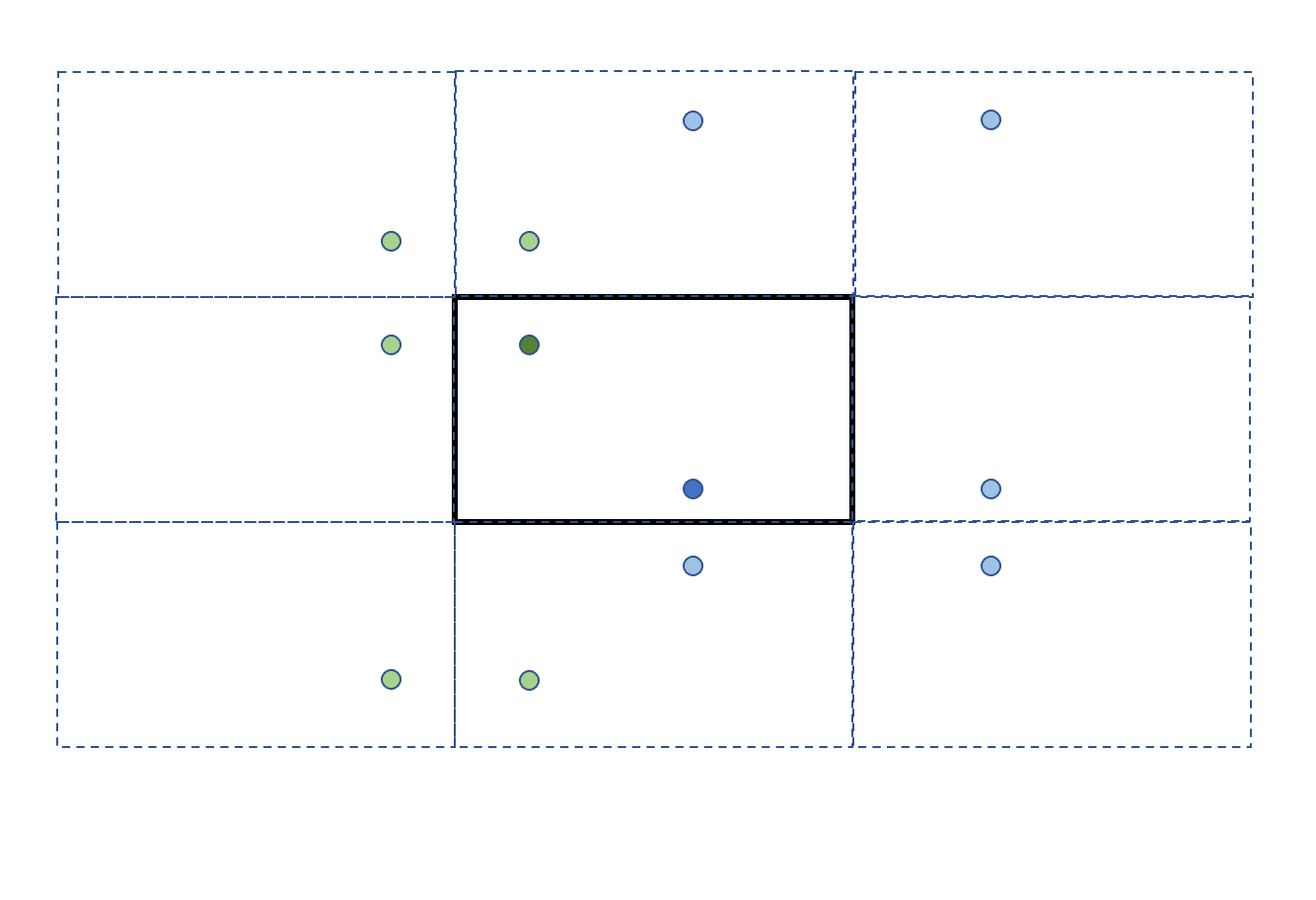
1. Create an infinite grid of copies of the room by mirroring the room, with the original room in the center. Each copy gets a copy of Ax (but not of Larry). Now there's a 1:1 correspondence between the possible attacks and the straight lines from Ax copies to Larry.

2. Consider the set of midpoints of those straight lines, reflected back to the original rectangle.
   They form 16 distinct points. Why only 16? It turns out that if you move by 4 rooms on the infinite grid in any direction, the midpoint (reflected back) is the same. Consider for instance the grid at (0,0) (the original room) vs (4,0). The midpoint lies in the room at (2,0), which has the same layout as the original room (because it was mirrored twice). That's why situation from (4,0) is basically like a magnified version of the original situation at (0,0). A similar argument can be made for moving by 4 rooms in any other direction. Hence it is sufficient to consider any 4x4 square of rooms.

If you are interested, I wrote a few lines of code to compute the coordinates that I'm happy to share.
||