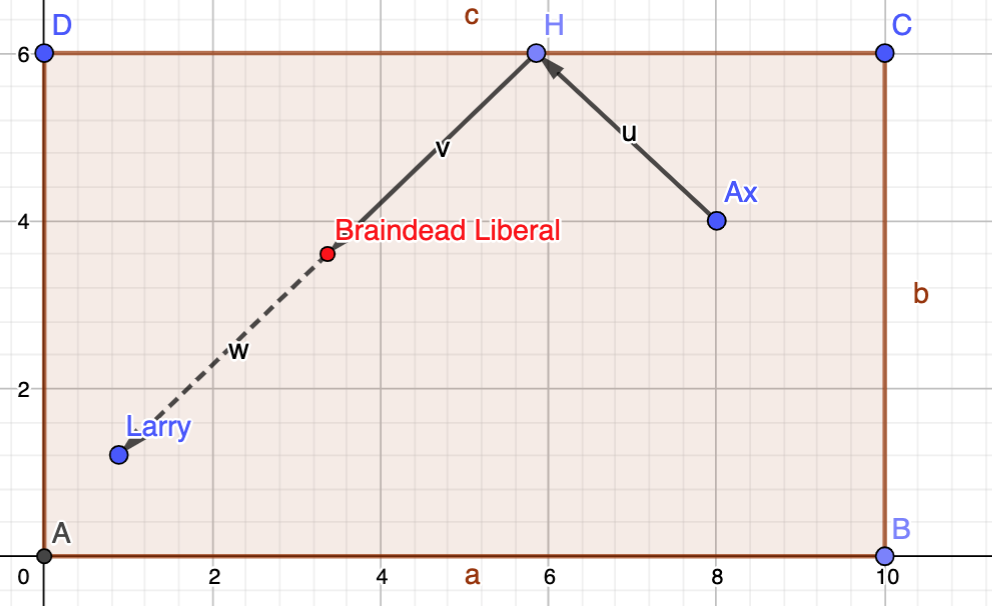
Puzzle time - don't waste braindead liberals
-
Finally I think I have it.
Lets call A0 Ax's actual position and A1 through A4 his reflected position off of each of the four mirrors. Same idea with L0-4.
Draw out those 10 points, and draw the 25 line segments that start from Ax and all 4 of his reflections and go to Larry and all four of his reflections. Now, all but one of these segments will extend outside the arena, but the ones that do are the equivalent of a 'bank shot' encompassing one or more reflections in the mirrored surface.
You can translate the midpoint of each of these segments to it's equivalent point within the arena, bu recognizing that it is the mirror image of the point across the nearest wall of the arena.
This will get you 25 points within the arena. You soon notice that 9 of these fall out of duplicates. So you are left with 16. They seem to form a neat grid.
I've not yet shown here that those 16 points are sufficient, though I convinced myself that as long as you choose the midpoints, you will also block equivalent shots between more distant reflections, which correspond to more zig-zaggy bank shots between Larry and Ax.
For example, here I have shown visually how Ax shooting Larry's reflection in the bottom mirror is equivalent to him shooting actual Larry with the bank shot:
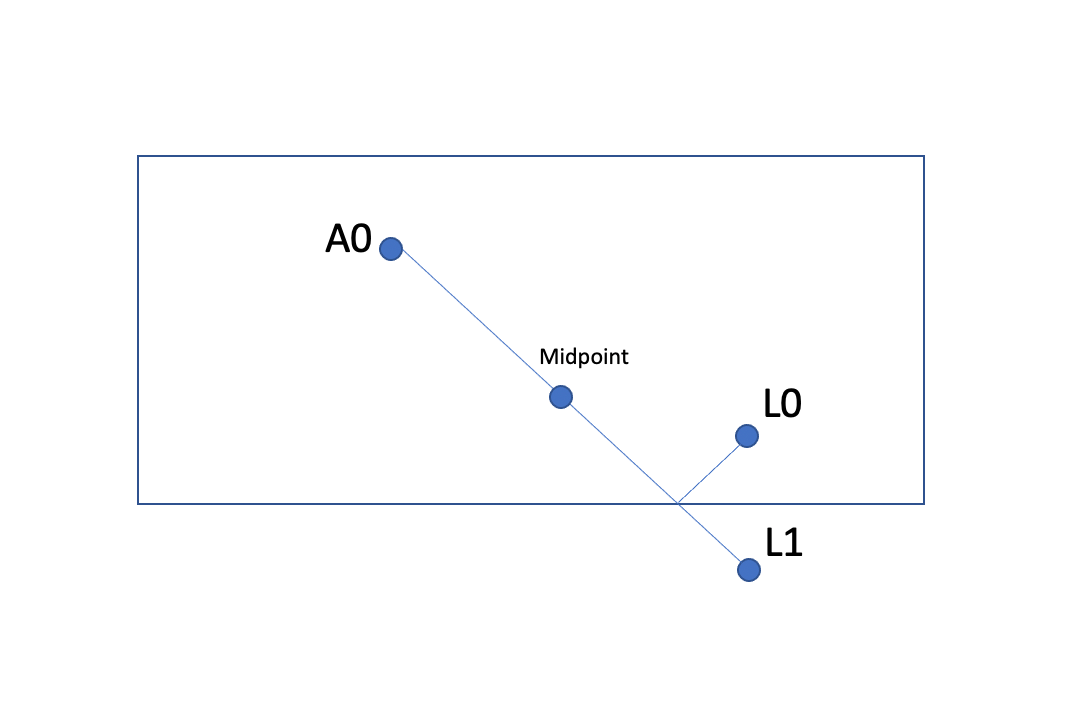
But more than that, you see that the midpoint will also block the case where Ax shoots Larry using the same two walls, but does three banks instead of 1. Note this corresponds to Ax's reflection A1 shooting Larry's reflection L2:
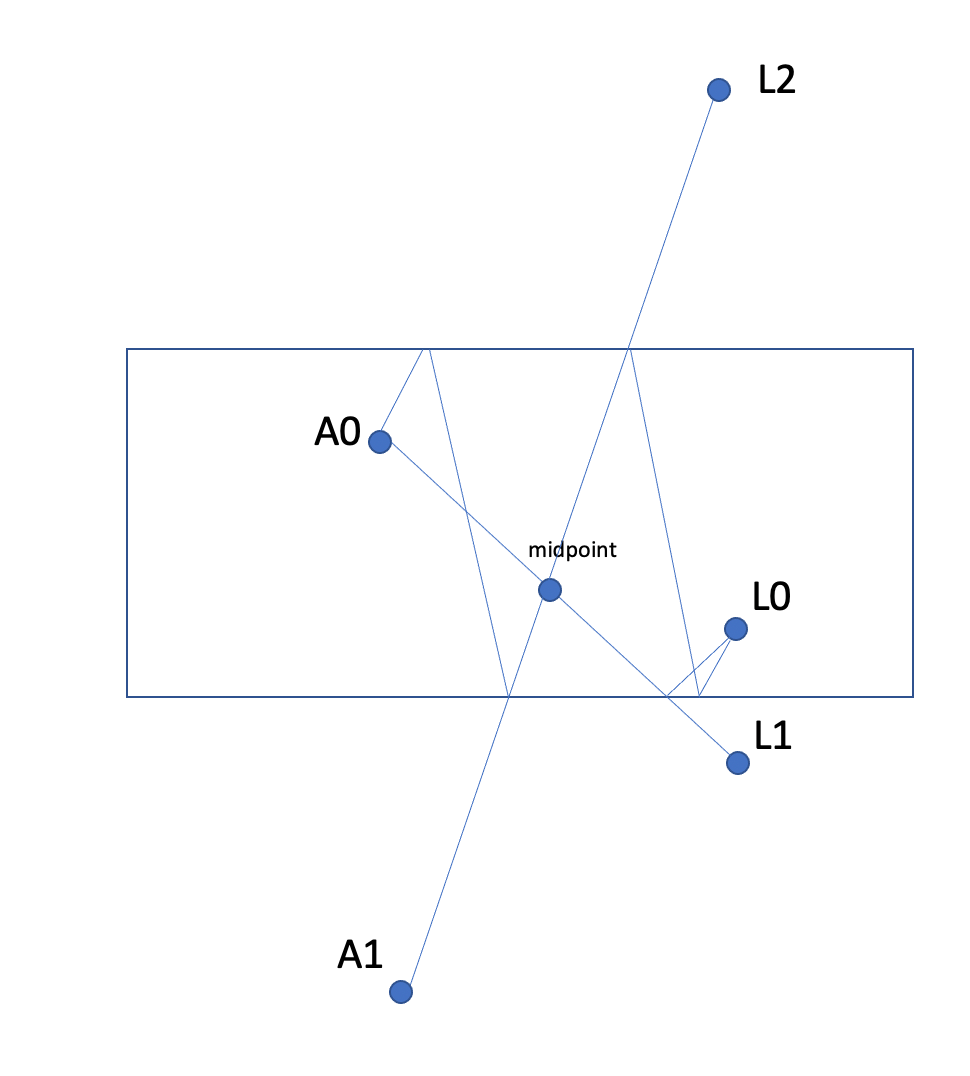
That point will stop all of the shots using just those two walls using an odd number of reflections. A distinct point will stop all that use an even number of reflections.
-
Yes so the midpoints, shifted if necessary, of the following segments:
A0-L0
A0-L1
A0-L2
A0-L3
A0-L4
A1-L2
A1-L3
A1-L4
A2-L3
A2-L4
A3-L4Where A0 and L0 are the positions of Ax and Larry respectively. and A1-4 and L1-4 are their apparent positions in the 4 mirrors that surround them.
-
If you want some data to play around with: I wrote down 10 lines of code to help me verify my method, which also supports your approach without many modifications (which shows that you are not far off from mine).
For instance, for this setup:
larry = (1.0,2.0) ax = (8.0,5.0) width = 10.0 height = 6.0your approach yields the following 25 midpoints:
[(4.5,3.5),(4.5,7.5),(4.5,1.5),(13.5,3.5),(3.5,3.5),(4.5,4.5),(4.5,8.5),(4.5,2.5),(13.5,4.5),(3.5,4.5),(4.5,-1.5),(4.5,2.5),(4.5,-3.5),(13.5,-1.5),(3.5,-1.5),(6.5,3.5),(6.5,7.5),(6.5,1.5),(15.5,3.5),(5.5,3.5),(-3.5,3.5),(-3.5,7.5),(-3.5,1.5),(5.5,3.5),(-4.5,3.5)]which, when shifted back, yield these 11 coordinates for BDLs:
[(3.5,1.5),(3.5,3.5),(3.5,4.5),(4.5,1.5),(4.5,2.5),(4.5,3.5),(4.5,4.5),(5.5,3.5),(6.5,1.5),(6.5,3.5),(6.5,4.5)] -
OK, so this is what I got.
||
-
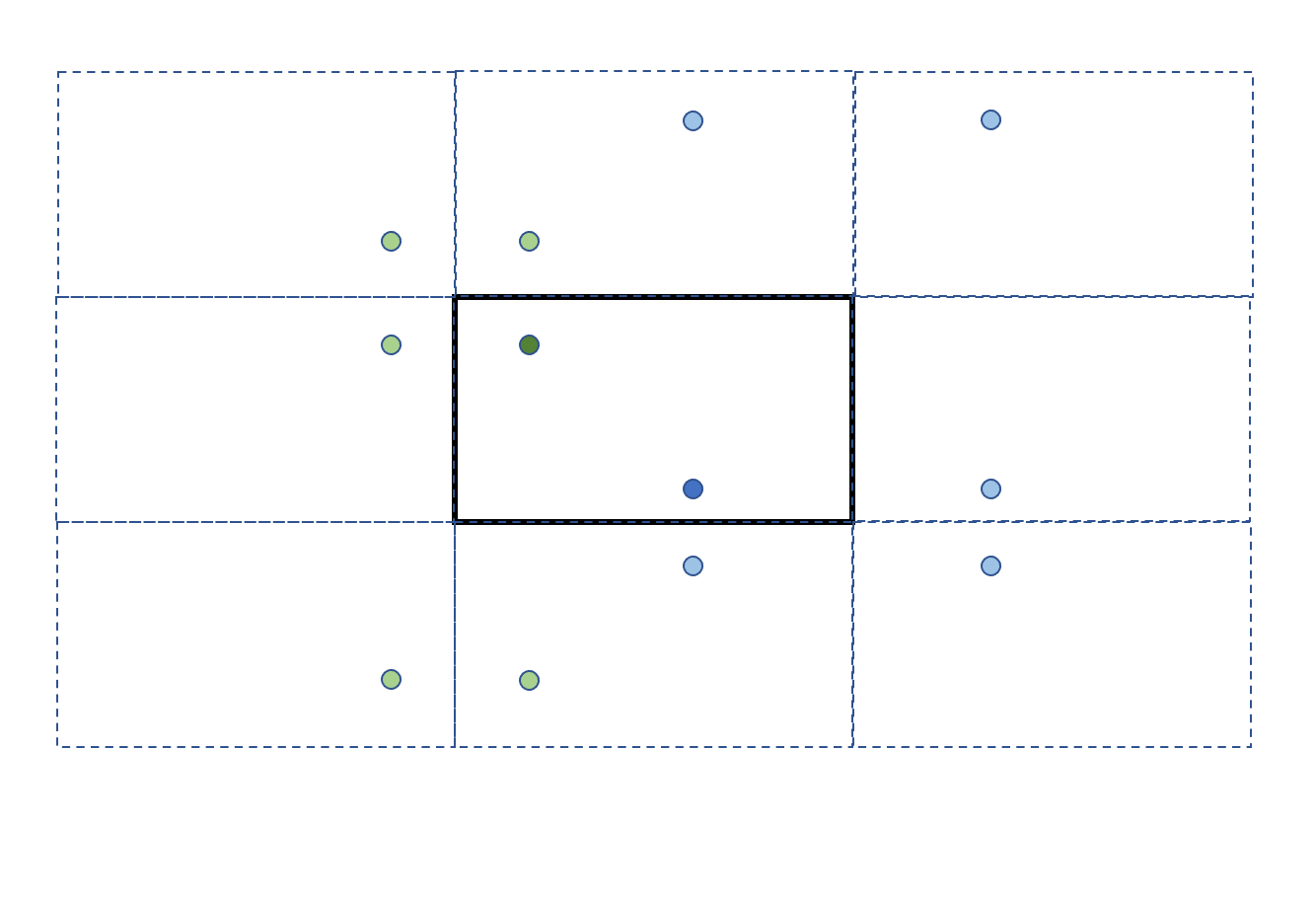
Create an infinite grid of copies of the room by mirroring the room, with the original room in the center. Each copy gets a copy of Ax (but not of Larry). Now there's a 1:1 correspondence between the possible attacks and the straight lines from Ax copies to Larry.
-
Consider the set of midpoints of those straight lines, reflected back to the original rectangle.
They form 16 distinct points. Why only 16? It turns out that if you move by 4 rooms on the infinite grid in any direction, the midpoint (reflected back) is the same. Consider for instance the grid at (0,0) (the original room) vs (4,0). The midpoint lies in the room at (2,0), which has the same layout as the original room (because it was mirrored twice). That's why situation from (4,0) is basically like a magnified version of the original situation at (0,0). A similar argument can be made for moving by 4 rooms in any other direction. Hence it is sufficient to consider any 4x4 square of rooms.
If you are interested, I wrote a few lines of code to compute the coordinates that I'm happy to share.
|| -