Puzzle time - odd run of heads
-
:::
You didn't specify that the solution must be analytic, so...Just for the heck of it, I thought this might be a good excuse to play around with WebPPL.
This is the distribution and expected value I got.
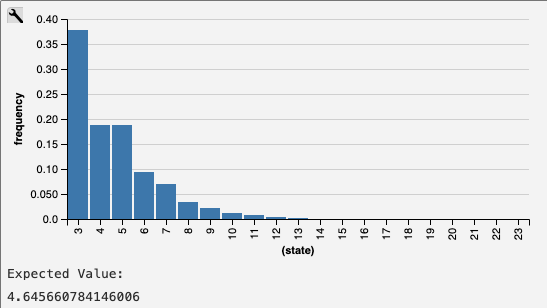
The model I used was this. You can just copy&paste it to http://webppl.org/ and play around with it, if you want to get an impression of what probabilistic programming is.
var oddrun = function() { var fluntil = function() { flip(.5) ? fluntil() + 1 : 1 } var flodd = function() { if (flip(.5)) { return { success : false , l : 1} } else { var r = flodd(); return { success : !(r.success), l : r.l+1 } ; } } var run = function() { var r = flodd() return r.success ? r.l : r.l + run() }; var l = fluntil() return l + run() } var dist = Infer( {method: 'enumerate', maxExecutions: 50000}, oddrun); viz.auto(dist); display("Expected Value:") display(expectation(dist)):::
-
:::
You didn't specify that the solution must be analytic, so...Just for the heck of it, I thought this might be a good excuse to play around with WebPPL.
This is the distribution and expected value I got.

The model I used was this. You can just copy&paste it to http://webppl.org/ and play around with it, if you want to get an impression of what probabilistic programming is.
var oddrun = function() { var fluntil = function() { flip(.5) ? fluntil() + 1 : 1 } var flodd = function() { if (flip(.5)) { return { success : false , l : 1} } else { var r = flodd(); return { success : !(r.success), l : r.l+1 } ; } } var run = function() { var r = flodd() return r.success ? r.l : r.l + run() }; var l = fluntil() return l + run() } var dist = Infer( {method: 'enumerate', maxExecutions: 50000}, oddrun); viz.auto(dist); display("Expected Value:") display(expectation(dist)):::
-
Oh right, I think there was a missing plus sign in my model, which I've now fixed.
This is what I get now.
:::
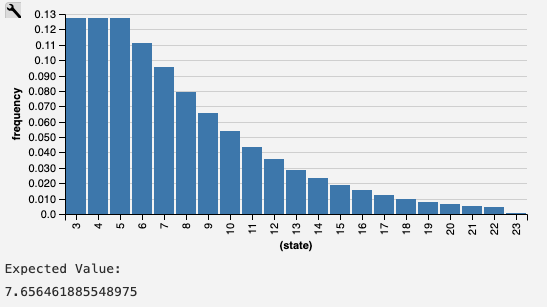
This looks right to me. The probability of THT is 1/8. The probability of TTHT or HTHT is 1/16, with a combined probability of 1/8.
My take for an analytic solution would be to count how many "winning" sequences of length n there are (let's call this q(n)) and then compute the limit of the sum of all i*q(i) / (2^i)
(for i = 1 to infinity) to get the expected value. Obviously, q(1)=0, q(2) = 0, q(3) = 1 and q(4) = 2. From the distribution diagram above I infer q(5) = 4 and q(6) = 7.This looks suspiciously similar to the Fibonacci sequence minus one.
:::
-
:::
That's the limit of the sum of all i*(Fib(i)-1) / (2^i). The main insight is that the number of "winning" sequences of length i is Fib(i)-1.
I don't really have an argument why it needs to be Fib(i)-1 (except the "abductive reasoning" rationale above), but I'm pretty confident that it is correct.
:::