Puzzle time - don't waste braindead liberals
-
wrote on 14 Oct 2020, 23:23 last edited by
For those who need an additional big hint. Don't look if you want the full fun
||
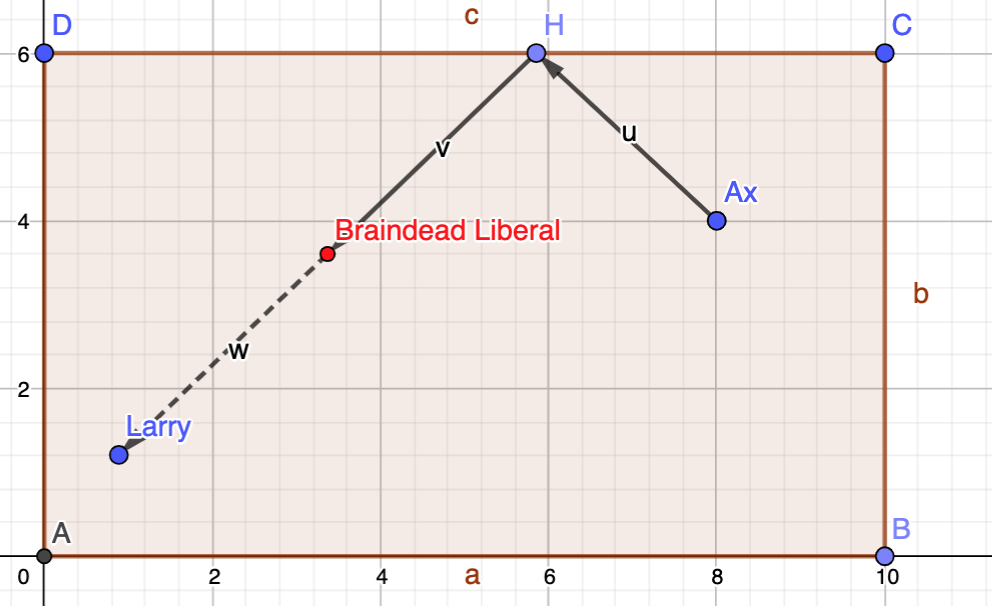
Here's an example of how to place BDLs - in this case 16 - that will prevent any attack, regardless of how many bounces. One possible attack with two bounces is indicated in the drawing. The coordinates of the BDLs as well as Ax and Larry can also be seen. Try it out. It's a safe position for Larry.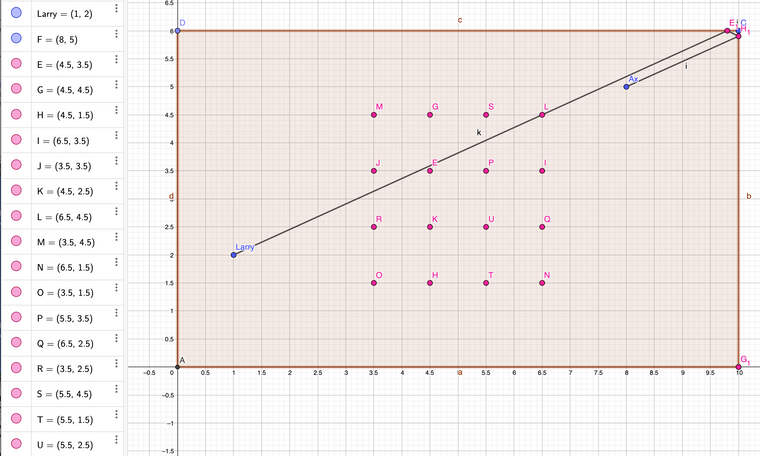
||
-
wrote on 15 Oct 2020, 01:21 last edited by
Have to think more, but it seems like it would be a large number. Just thinking out loud, if Ax shoots almost horizontal, but a small angle less than that, the back and forth an infinite number of times.
Anyway, have to think more. (But still probably won't be able to discover the answer 55555)
-
wrote on 15 Oct 2020, 18:51 last edited by
I wouldn't need to move. I'd simply stare at him and tell him if he moves an inch I'm going to break the rules and go over and slap him into next week, and he would shit himself and pass out.
Then I'd come looking for the guy who put me in a room with Ax.
-
wrote on 15 Oct 2020, 18:58 last edited by
@George-K said in Puzzle time - don't waste braindead liberals:
@Klaus , you and @jon-nyc need to get a room.
SRSLY
Preferably one with big fuckoff lasers in it.
-
wrote on 15 Oct 2020, 20:34 last edited by
Don’t post an answer yet I want to play with this tonight.
-
wrote on 15 Oct 2020, 21:54 last edited by
Are the brain dead liberals the same size as Larry? They’re likely vegan, and tiny little things...
-
wrote on 15 Oct 2020, 22:33 last edited by
Indeed. So tiny that they have no extension.
-
wrote on 16 Oct 2020, 04:14 last edited by
Does Larry have to worry about shooting himself?
-
wrote on 16 Oct 2020, 04:28 last edited by
I’m guessing it’s a countably infinite answer that is related to the primes but I still need to work on it.
-
wrote on 16 Oct 2020, 04:30 last edited by
No, it's a very finite number.
-
wrote on 16 Oct 2020, 04:48 last edited by
Ok. I think I can see that now... more tomorrow
-
wrote on 16 Oct 2020, 09:35 last edited by Klaus
This puzzle can be solved using high school math and geometry knowledge. Actually, basically no math/geometry is involved apart from knowing how a mirror reflects a laser (incoming angle = outgoing angle).
I can add a few more hints if it is too hard (well, it is hard).
-
wrote on 16 Oct 2020, 09:55 last edited by
Don’t add any hints
-
wrote on 16 Oct 2020, 10:42 last edited by
-
wrote on 16 Oct 2020, 11:21 last edited by
I’ve almost got this just need to figure out one last piece when I can get to a desk
-
wrote on 16 Oct 2020, 11:52 last edited by Klaus
@jon-nyc said in Puzzle time - don't waste braindead liberals:
I’ve almost got this just need to figure out one last piece when I can get to a desk
Reminds me of a famous quote from Fermat from 1637.
I have discovered a truly marvelous proof of this, which this margin is too narrow to contain
The proof of his famous conjecture was written down in 1995 after thousands of mathematicians spend their whole life working on the maths necessary to make that proof.
-
wrote on 17 Oct 2020, 13:19 last edited by jon-nyc
Finally I think I have it.
Lets call A0 Ax's actual position and A1 through A4 his reflected position off of each of the four mirrors. Same idea with L0-4.
Draw out those 10 points, and draw the 25 line segments that start from Ax and all 4 of his reflections and go to Larry and all four of his reflections. Now, all but one of these segments will extend outside the arena, but the ones that do are the equivalent of a 'bank shot' encompassing one or more reflections in the mirrored surface.
You can translate the midpoint of each of these segments to it's equivalent point within the arena, bu recognizing that it is the mirror image of the point across the nearest wall of the arena.
This will get you 25 points within the arena. You soon notice that 9 of these fall out of duplicates. So you are left with 16. They seem to form a neat grid.
I've not yet shown here that those 16 points are sufficient, though I convinced myself that as long as you choose the midpoints, you will also block equivalent shots between more distant reflections, which correspond to more zig-zaggy bank shots between Larry and Ax.
For example, here I have shown visually how Ax shooting Larry's reflection in the bottom mirror is equivalent to him shooting actual Larry with the bank shot:
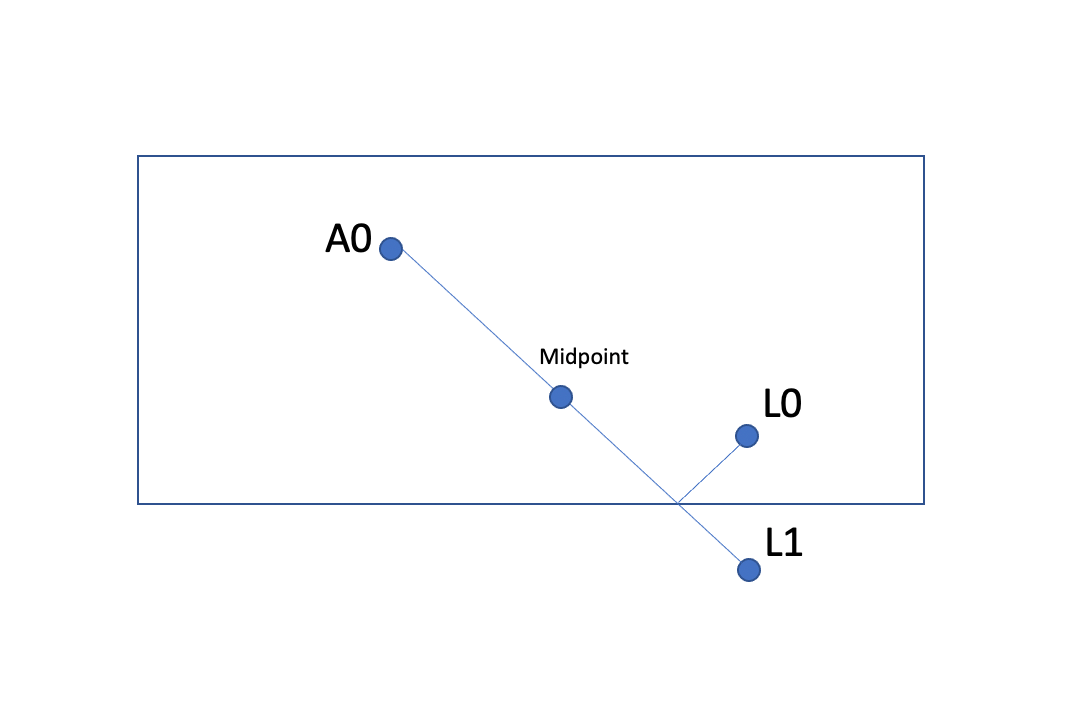
But more than that, you see that the midpoint will also block the case where Ax shoots Larry using the same two walls, but does three banks instead of 1. Note this corresponds to Ax's reflection A1 shooting Larry's reflection L2:
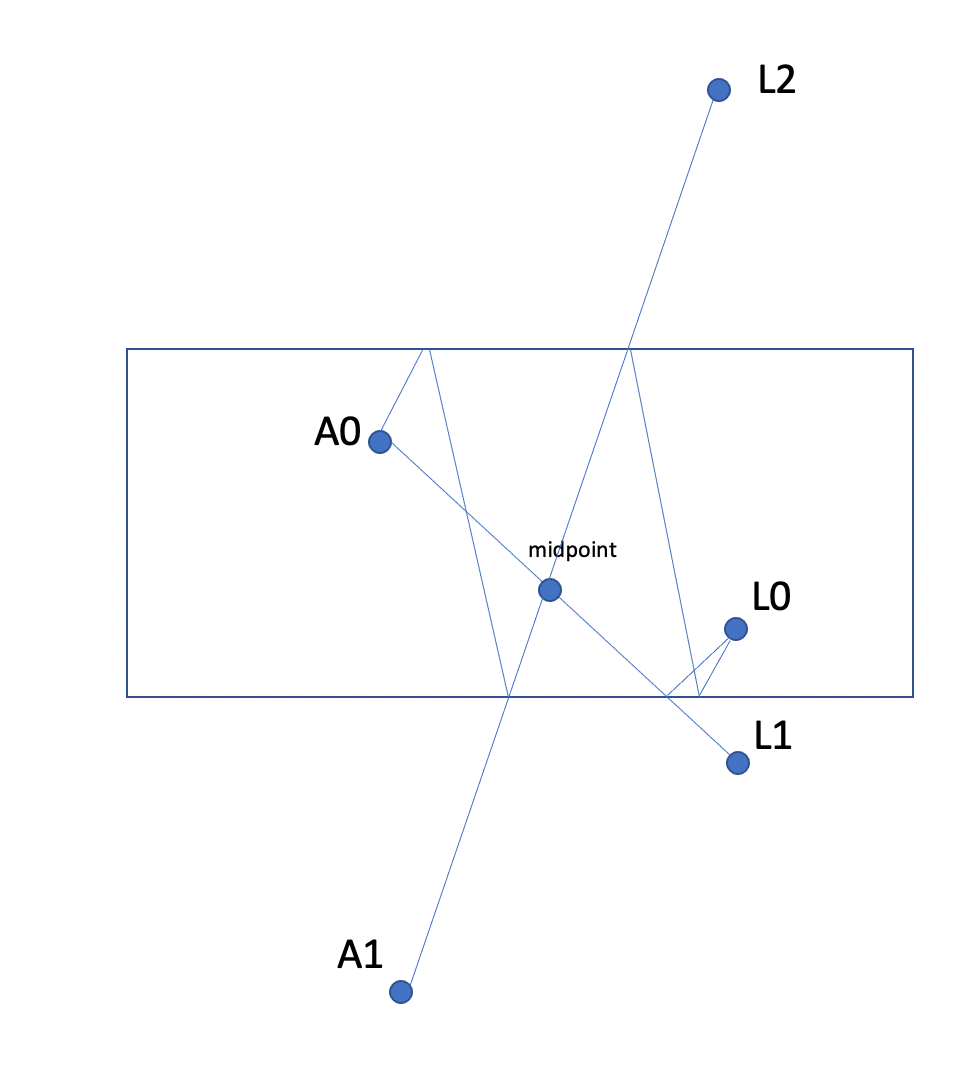
That point will stop all of the shots using just those two walls using an odd number of reflections. A distinct point will stop all that use an even number of reflections.
-
wrote on 17 Oct 2020, 13:43 last edited by
That wasn’t correct. I need to fix it and repost.
-
wrote on 17 Oct 2020, 15:27 last edited by Klaus
You are close. Many right ideas in your draft.
