Geometry problems ...
-
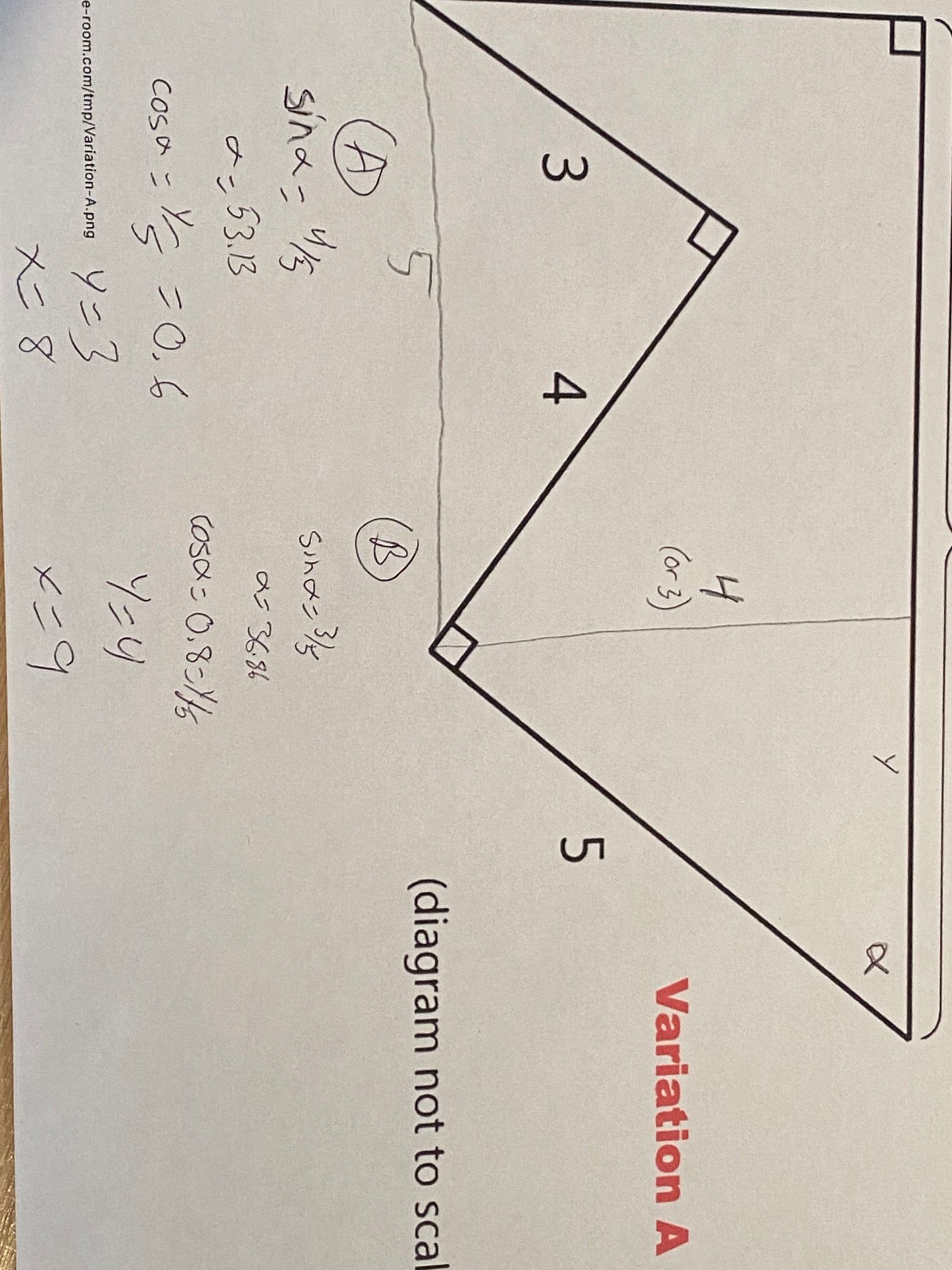
Variation-A could be solved using only simple geometric understanding without actually doing any computation. I first solved it using the Pythagorean Theorem then later realized that even using the Pythagorean Theorem was unnecessary.
Variation-B, I had to use the Pythagorean Theorem twice to get to the value of x.
I will post my solutions later tonight (Eastern Time), so other people have a chance to solve this during the day without spoiler.
-
Thinking a little more about it, I found a nice geometric solution using ruler and compass.
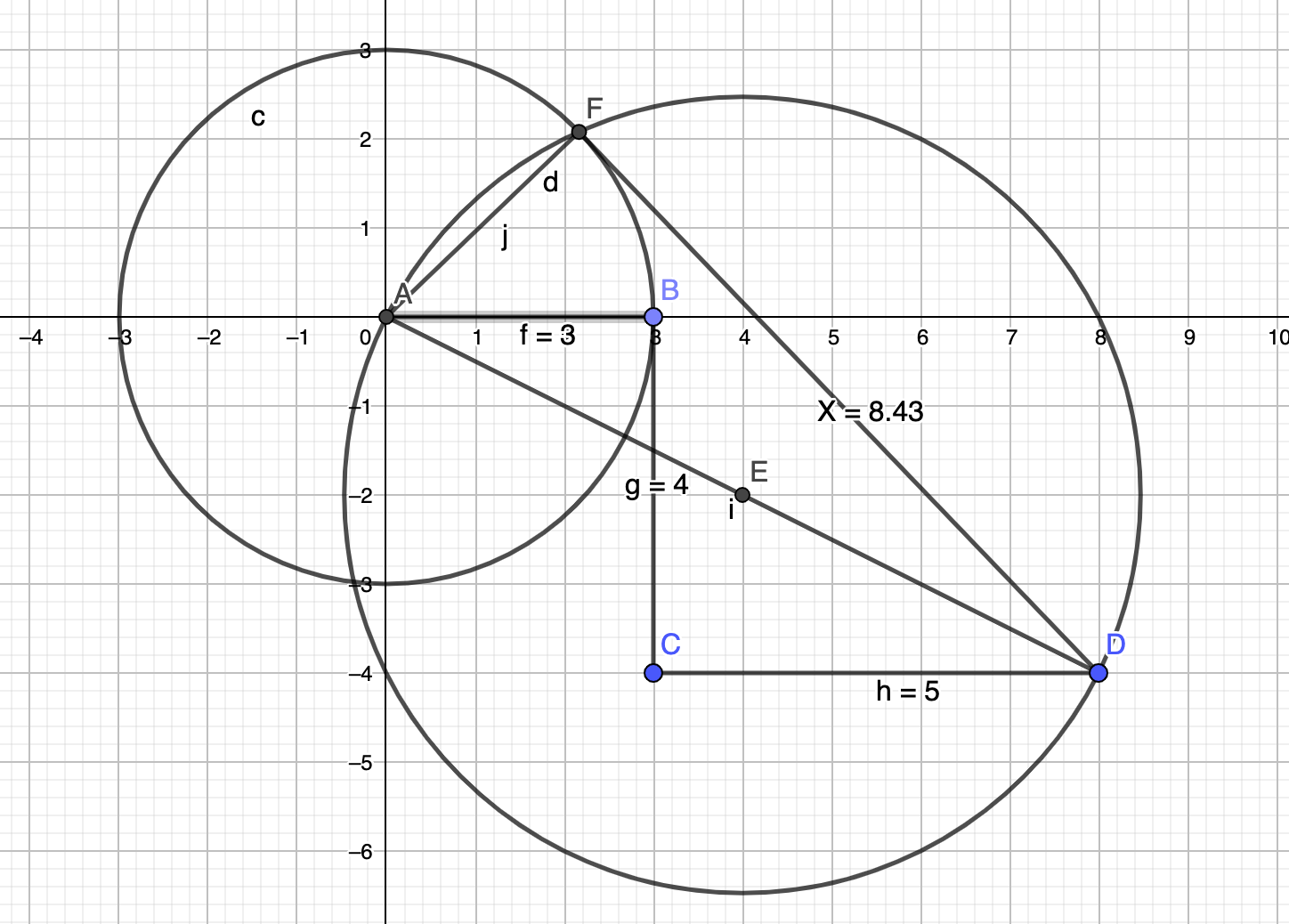
Here's the geometric solution for the second task.
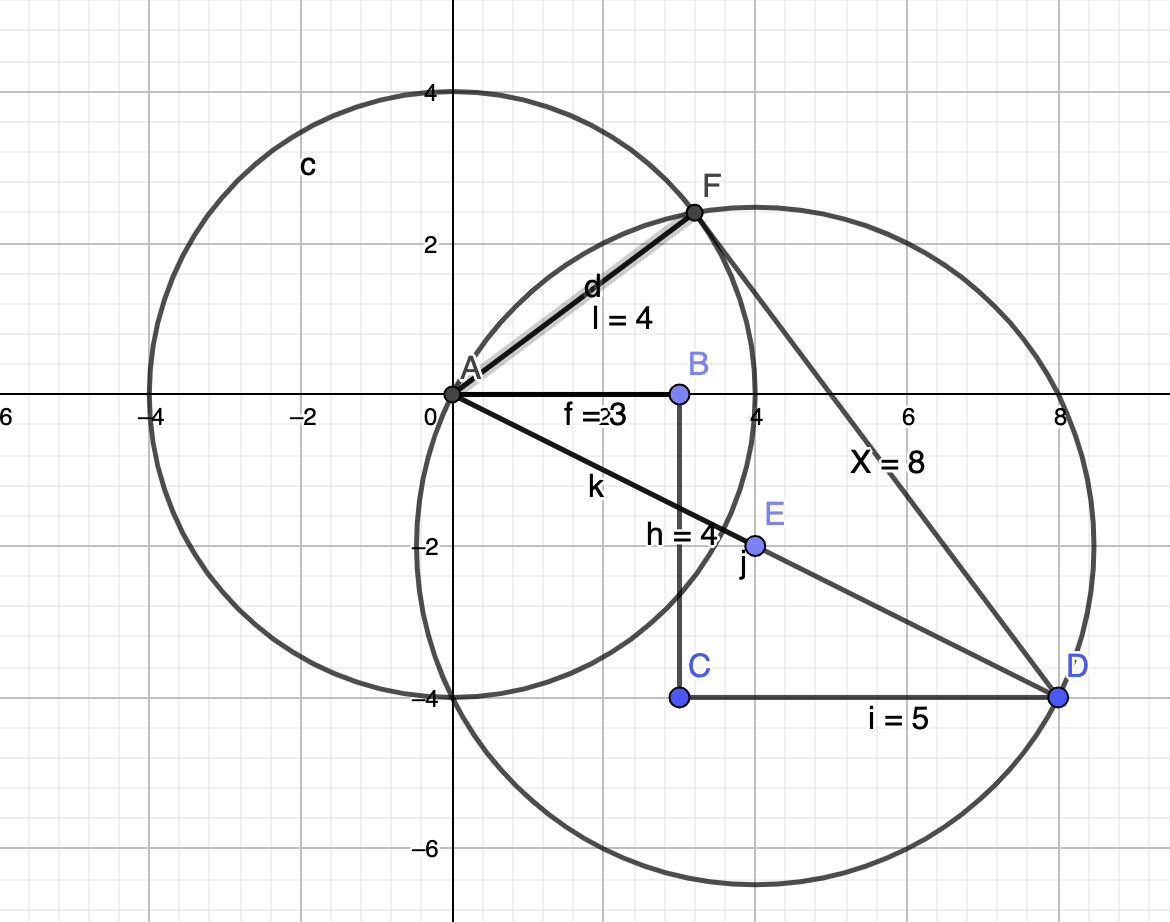
This is really nice since it involves the famous Thales circle.Here's how to construct it.
Draw the points and segments A-B-C-D. The lengths are given in the task; the angles are rectangular.
Now draw a circle of radius 4 (radius 3 for the second task) around A.
Take the segment between A and D. The middle of that segment (which is constructible ) is the center of another circle whose diameter is the distance between A and D.
That's the "Thales circle". Any point on that circle yields a rectangular triangle. Hence we take the intersection between the two circles. Hence
the intersection between the two circles is the desired missing point F. The distance from F to D is the desired length X. -
well the length of the line from the bottom left vertex to the top right vertex can be computed directly as the hypotenuse of a right triangle with the other two sides of length 8 and 4. That length gives you two lengths of a right triangle - 4 and that length in A, or 3 and that length in B. The third length is x. it's then an algebra problem using pythagoras. That method should work for both problems. Not elegant but not too complicated.
-
@Horace said in Geometry problems ...:
well the length of the line from the bottom left vertex to the top right vertex can be computed directly as the hypotenuse of a right triangle with the other two sides of length 8 and 4.
I don't think so. Why should the length of the other side be 8?
-
I'm sliding the length 4 segment (the one in the middle) down the length 5 segment by 3 units so the length 4 segment touches the left vertical. That gives a right triangle of side lengths 4, 8, and sqrt(80). sqrt(80) is the hypotenuse of the right triangle with other lengths y and x, where y is either 3 or 4 in the two problems and x is the answer.
-
Ax's method for problem A probably starts with the 8/4 right triangle idea and from there finds that x must be 8 because there are then two symmetric right triangles with their hypotenuses, er hypoteni, in common, and we know both have equal lengths of 4 for the short side and they must also have equal length for the long non-hypotenuse side, which in that case is 8, by the original idea of constructing the 8/4 triangle.
-
My solution to Variation-A:

The black outline polygon ABCDE is the information provided in the problem.
- Use the information from the BCDE line segments to construct the BF(D)E triangle.
- Realize that the BAE triangle is congruent to the BFE triangle.
- Hence the length of FE equals the length of AE, x = 8
-
My solution for Variation-B, as mentioned before, need to apply the Pythagorean Theorem twice, but it is essentially the same as already described by @Horace (4 posts above, and 6 posts above).
Some one made YouTube video that very nicely illustrated that solution:
Link to video
I got these two problems from that YouTube video.