Puzzle time: the baseball fan
-
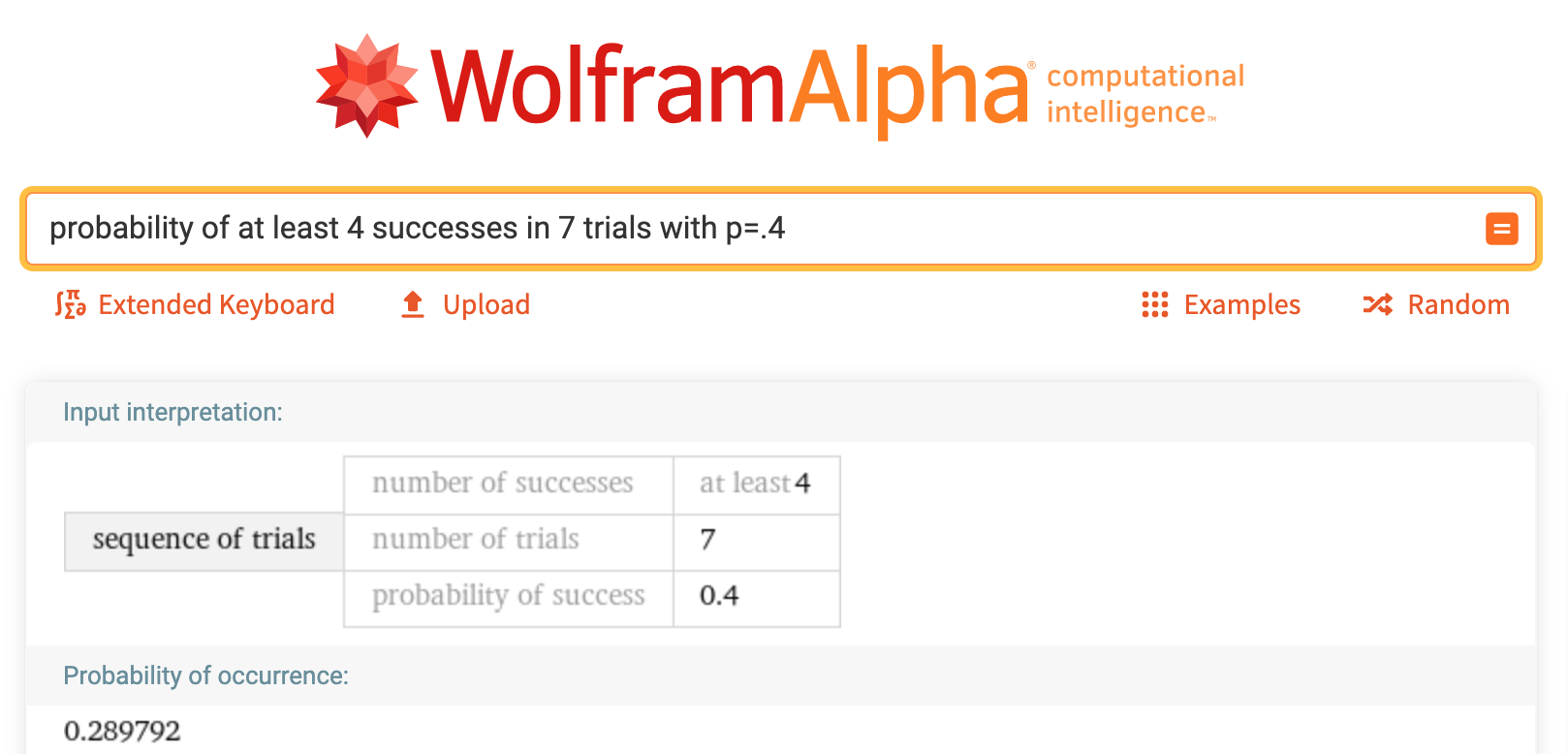
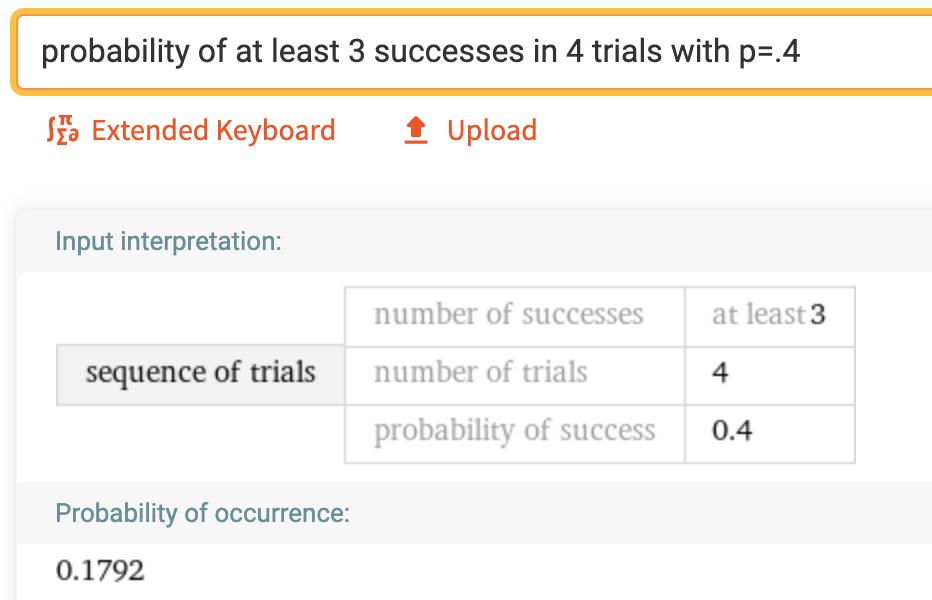
You are a rabid baseball fan and, miraculously, your team has won the pennant — thus, it gets to play in the World Series.
Unfortunately, the opposition is a superior team whose probability of winning any given game against your team is 60%.
Sure enough, your team loses the first game in the best-of-seven series.
You leave for a camping trip and, upon your return, you run out into the street and grab the first passerby. "What happened in games 2 and 3 of the World Series?"
"They were split," he says. "One game each."
Should you be happy?
-
Thought this was going to be about the 69 Mets who lost their first game. But then they swept past the Orioles.
FTW
-
I should be more specific
Link to video -
-
Well, you didn't specify what "Should you be happy?" means.
If I were a stoic, for instance, all that would matter to make me happy was whether the team played as well as they could, and it wouldn't matter whether they won or lost.
I figured that "one game each" is better than what is to be expected at the given odds, hence one should be happy.
But you seem to mean something else.
-
You know what's funny?
My kid's old math circle mailed this question out Sunday. I have nobody to ask any clarifying questions of, they send out hints Tuesday and Thursday and an answer Saturday. But somehow I managed.
I think there's a skill called 'questionology' that I'm apparently better at than you and Ax.
-
You guys should become a comedy troupe!!!


-
You know what's funny?
My kid's old math circle mailed this question out Sunday. I have nobody to ask any clarifying questions of, they send out hints Tuesday and Thursday and an answer Saturday. But somehow I managed.
I think there's a skill called 'questionology' that I'm apparently better at than you and Ax.
@jon-nyc said in Puzzle time: the baseball fan:
I think there's a skill called 'questionology' that I'm apparently better at than you and Ax.
The difference is that you know you have nobody to ask for clarification, whereas for us its a small investment to ask a clarifying question compared to investing valuable brain time for questionology. You are not better; you are just in a situation with less options