Puzzle time - How many bits
-
Here's a solution that gets it with three bits every time:
:::
K and H have prearranged a mapping of teams to 4 bit binary codes. K sends a two bit message to H indicating a bit where the two teams' digital representation differs. H responds with the value of that bit. That gives K the answer in 3, every time.
:::
@jon-nyc said in Puzzle time - How many bits:
Here's a solution that gets it with three bits every time:
:::
K and H have prearranged a mapping of teams to 4 bit binary codes. K sends a two bit message to H indicating a bit where the two teams' digital representation differs. H responds with the value of that bit. That gives K the answer in 3, every time.
:::
:::
How does it work when two teams’ binary representation differ by two or more bits?
:::
-
Here's a quite simple strategy with an expected number of bits of only 1.875.
H sends 0 if the winner is in the first half and 1 else.
With probability 0.5 K knows the winner after this one bit.
Then H sends 0 if the winner is in the first half of the remaining half and 1 else.
With probability 0.25 K knows the winner after the second bit.
Continuing similarly, K knows the winner after 3 bits with probability 0.125 and after 4 bits with 0.125.
On average, that makes 1.875 bits.
One slightly inelegant aspect of the approach is that H doesn't know when to stop sending bits.
-
I vaguely remember working on exercise sheets about Huffman coding during my studies, which would be directly applicable to this task if probability distributions were known. The idea is to have a "prefix-free" code that assigns short codes to frequently occuring outcomes/symbols. Prefix-free means that the code for one symbol is never a prefix of another code, which is necessary to make sure that a bit stream can be decoded (otherwise you wouldn't know when a code ends).
For instance, given a typical frequency distribution of letters in written text, here's a Huffman code for letters.
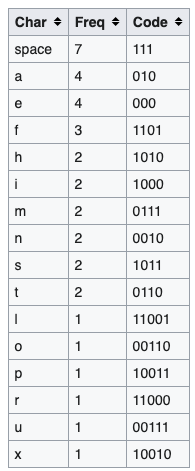
-
An addendum to that that keeps max 3 but makes the expected value less than 2.5:
:::
Instead of always sending 2 bits to indicate the differing digit every time, send only one bit if it's bit 0 or 1. In other words, send:
0 -> 1st bit
1 -> 2nd bit
10 -> third bit
11 -> 4th bitI don't feel like calculating the exact expected value, but given that many pairs of digital words will differ in multiple places, you can always choose to send the more efficient representation when possible. Therefore it should be < 2.5.
:::
@jon-nyc said in Puzzle time - How many bits:
An addendum to that that keeps max 3 but makes the expected value less than 2.5:
:::
Instead of always sending 2 bits to indicate the differing digit every time, send only one bit if it's bit 0 or 1. In other words, send:
0 -> 1st bit
1 -> 2nd bit
10 -> third bit
11 -> 4th bitI don't feel like calculating the exact expected value, but given that many pairs of digital words will differ in multiple places, you can always choose to send the more efficient representation when possible. Therefore it should be < 2.5.
:::
So I decided to do the quick math, only 48 of 240 team pairs would differ only on the third or fourth bit, do this method would have an expected value of 2.2.
-
@jon-nyc said in Puzzle time - How many bits:
@Klaus Interesting. I had never heard of Huffman codes.
Amazingly, this stuff was developed in the 1950s already.
I find it amazing how many seemingly modern concepts are in fact pretty old.
For instance, in my field, many of the main concepts we use to design programming languages stem from the 1930s and 1940s, well before computers were even invented.
This taught me to never underestimate the power of a smart person equipped with a pencil and a piece of paper. You can change the world with a pencil.
-
Nice solution jon.
I wonder if it would be possible to divide the 120 pairs into four sets, where in each set, any team appearing within it must always be either the first of the pair, or the second. That would lead to a solution in three bits. The person who knows the pair would message the set number, while the person who knows the winner would message whether the winner is first or second in its pairs within that set.
-
Official solution:
SOLUTION: Romeo and Juliet can, in advance, label the 16 teams (in alphabetic order, perhaps) by the binary numbers 0000 through 1111. Then, when the time comes, Romeo can send Juliet eight bits: the four bits corresponding to one team, and the four bits corresponding to the other one. Juliet can then send back a 0 if the winning team was the one with the smaller number, and a 1 otherwise. That comes to nine bits, and we can trim that to 8 by noting that the number of unordered pairs of teams is only 16 x 15/2 = 120 which is less than 2 to the seventh power, thus Romeo can code the matchup with only seven bits.
But an easier and faster solution is to just have Juliet send Romeo the four bits corresponding to the winning team. Surely, we can't do any better than four bits, right?
Amazingly, we can! We can name those four positions in the team codes (leftmost, next-to-left, next-to-right, rightmost) by, say, 00, 01, 10, and 11 respectively. The codes of the two playing teams must differ in at least one of the four positions; Romeo picks such a position and sends its name (two bits) to Juliet. She now only needs to look at the value of the bit in that position of the winning team and send it to Romeo. Three bits total!
For example, suppose the playing teams are 0010 and 0110, and 0110 won. The only position where the playing teams differ is the next-to-left, the "01" position, so Romeo must send "01" to Juliet. She checks the next-to-left position of the winning team — it is a "1" — and sends that "1" to Romeo. Done.
It can be shown that three bits is unbeatable. Note that in the most efficient communication scheme, more information is passed from the student to the teacher than vice-versa. Is there a lesson to be learned from that?
[Devised and communicated to me by Alon Orlitsky, of the University of California, San Diego.]