Puzzle time - How many bits
-
Does H know what K knows? Does H know what K wants to know? Can they have a common strategy they both know about?
-
@klaus said in Puzzle time - How many bits:
@klaus said in Puzzle time - How many bits:
Does H know what K knows?
In that case, one bit would be sufficient. If both know it must be team A or team B, then H can send 0 for team A or 1 for team B.
The puzzle states that K knows the two teams but not the winner and H knows only the winner but not the other team. What they both know in advance are the 16 possible teams and whatever strategy they devise.
-
Hm. I think this one would work with two bits, but it would only work in 75% of all cases.
:::
K asks one of two boolean questions:
- Even? - is the winning team on an even position
- Lower? - is the winning team among the lower half of team numbers
Transmitting the question requires one bit, the answer requires one bit.
Of course, K is screwed if both teams have equal parity and are in the same half.
:::and here's an extension of the idea with three bits that presumably works in 100% of all cases.
:::
K sends a second bit which asks H to either shuffle the team order or not before answering the question.
The shuffling is such that equal parity and equal half cannot happen in both the unshuffled and shuffled order. I'm not quite sure whether that's even possible, but let's call this a solution just for fucks sake!
::: -
@jon-nyc said in Puzzle time - How many bits:
In engineering school I used to wonder why you couldn't, in theory, send an unlimited amount of information on a superconducting channel just by setting the voltage a very precise amount, say 3.141592674......
Wouldn't the measurement influence the voltage? I guess that would be the main reason. Also, if you measure current, you'd at some point measure single electrons, which are discrete.
@klaus said in Puzzle time - How many bits:
@jon-nyc said in Puzzle time - How many bits:
In engineering school I used to wonder why you couldn't, in theory, send an unlimited amount of information on a superconducting channel just by setting the voltage a very precise amount, say 3.141592674......
Wouldn't the measurement influence the voltage? I guess that would be the main reason. Also, if you measure current, you'd at some point measure single electrons, which are discrete.
Yes, you can get precision only down to the Planck scale and then you're limited by Heisenberg's uncertainty principle.
-
@klaus said in Puzzle time - How many bits:
@jon-nyc said in Puzzle time - How many bits:
In engineering school I used to wonder why you couldn't, in theory, send an unlimited amount of information on a superconducting channel just by setting the voltage a very precise amount, say 3.141592674......
Wouldn't the measurement influence the voltage? I guess that would be the main reason. Also, if you measure current, you'd at some point measure single electrons, which are discrete.
Yes, you can get precision only down to the Planck scale and then you're limited by Heisenberg's uncertainty principle.
@axtremus said in Puzzle time - How many bits:
@klaus said in Puzzle time - How many bits:
@jon-nyc said in Puzzle time - How many bits:
In engineering school I used to wonder why you couldn't, in theory, send an unlimited amount of information on a superconducting channel just by setting the voltage a very precise amount, say 3.141592674......
Wouldn't the measurement influence the voltage? I guess that would be the main reason. Also, if you measure current, you'd at some point measure single electrons, which are discrete.
Yes, you can get precision only down to the Planck scale and then you're limited by Heisenberg's uncertainty principle.
My point was more immediate: Voltage is measured by sending a small current through a resistor. That current would necessarily cause a drop in the voltage.
-
Here's a solution that gets it with three bits every time:
:::
K and H have prearranged a mapping of teams to 4 bit binary codes. K sends a two bit message to H indicating a bit where the two teams' digital representation differs. H responds with the value of that bit. That gives K the answer in 3, every time.
:::
-
An addendum to that that keeps max 3 but makes the expected value less than 2.5:
:::
Instead of always sending 2 bits to indicate the differing digit every time, send only one bit if it's bit 0 or 1. In other words, send:
0 -> 1st bit
1 -> 2nd bit
10 -> third bit
11 -> 4th bitI don't feel like calculating the exact expected value, but given that many pairs of digital words will differ in multiple places, you can always choose to send the more efficient representation when possible. Therefore it should be < 2.5.
:::
-
I like your 3 bit solution, but the 2.5 bit one looks unsound.
If you send messages of variable length, you'd have to transmit the length of the message. Otherwise you could easily cheat by saying that "the empty message", for instance, also transmits information.
-
I like your 3 bit solution, but the 2.5 bit one looks unsound.
If you send messages of variable length, you'd have to transmit the length of the message. Otherwise you could easily cheat by saying that "the empty message", for instance, also transmits information.
-
Here's a solution that gets it with three bits every time:
:::
K and H have prearranged a mapping of teams to 4 bit binary codes. K sends a two bit message to H indicating a bit where the two teams' digital representation differs. H responds with the value of that bit. That gives K the answer in 3, every time.
:::
@jon-nyc said in Puzzle time - How many bits:
Here's a solution that gets it with three bits every time:
:::
K and H have prearranged a mapping of teams to 4 bit binary codes. K sends a two bit message to H indicating a bit where the two teams' digital representation differs. H responds with the value of that bit. That gives K the answer in 3, every time.
:::
:::
How does it work when two teams’ binary representation differ by two or more bits?
:::
-
Here's a quite simple strategy with an expected number of bits of only 1.875.
H sends 0 if the winner is in the first half and 1 else.
With probability 0.5 K knows the winner after this one bit.
Then H sends 0 if the winner is in the first half of the remaining half and 1 else.
With probability 0.25 K knows the winner after the second bit.
Continuing similarly, K knows the winner after 3 bits with probability 0.125 and after 4 bits with 0.125.
On average, that makes 1.875 bits.
One slightly inelegant aspect of the approach is that H doesn't know when to stop sending bits.
-
I vaguely remember working on exercise sheets about Huffman coding during my studies, which would be directly applicable to this task if probability distributions were known. The idea is to have a "prefix-free" code that assigns short codes to frequently occuring outcomes/symbols. Prefix-free means that the code for one symbol is never a prefix of another code, which is necessary to make sure that a bit stream can be decoded (otherwise you wouldn't know when a code ends).
For instance, given a typical frequency distribution of letters in written text, here's a Huffman code for letters.
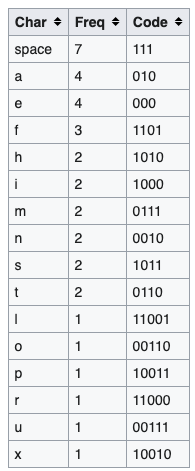
-
An addendum to that that keeps max 3 but makes the expected value less than 2.5:
:::
Instead of always sending 2 bits to indicate the differing digit every time, send only one bit if it's bit 0 or 1. In other words, send:
0 -> 1st bit
1 -> 2nd bit
10 -> third bit
11 -> 4th bitI don't feel like calculating the exact expected value, but given that many pairs of digital words will differ in multiple places, you can always choose to send the more efficient representation when possible. Therefore it should be < 2.5.
:::
@jon-nyc said in Puzzle time - How many bits:
An addendum to that that keeps max 3 but makes the expected value less than 2.5:
:::
Instead of always sending 2 bits to indicate the differing digit every time, send only one bit if it's bit 0 or 1. In other words, send:
0 -> 1st bit
1 -> 2nd bit
10 -> third bit
11 -> 4th bitI don't feel like calculating the exact expected value, but given that many pairs of digital words will differ in multiple places, you can always choose to send the more efficient representation when possible. Therefore it should be < 2.5.
:::
So I decided to do the quick math, only 48 of 240 team pairs would differ only on the third or fourth bit, do this method would have an expected value of 2.2.
 Spoiler Text
Spoiler Text