Puzzle time - Pi squared over six
-
:::
Investing a few
CPUbrain cycles, I'd say that the alternating series (swap every other sign) yields pi^2/12:If you subtract that number from pi^2/6 you get
(1+1/4 + 1/9 + 1/16 + ...) - (1 - 1/4 + 1/9 - 1/16 + ...) =
2*(1/4 + 1/16 + ...) =
1/2*(/1 + 1/4 + ...) = 1/2 * pi^2 /6 = pi^2 / 12.However, I'm not sure whether my calculation is mathematically sound. It is in general not valid to manipulate infinite sums in the way I do above.
:::
-
THat's good Klaus. You can generalize to k.
Let x be the value of the series with the + signs flipped to - signs at the 1/k^2 term, 1/(2k)^2 term and so on, every kth term. Then calculate pi^2/6 - x .
(pi^2)/6 - x
= 2 * (1/k^2 +1/(2k)^2 + ... )
= (2/k^2)(1 + 1/2^2 + 1/3^2 + ...)
= (2/k^2) * ((pi^2/6))So x = ((pi^2/6)) * (1 - 2/k^2). Done.
Your example:
1 - 1/2^2 + 1/3^2 - 1/4^2 + ...
= (pi^2)/12 -
I used to love messing around with this sort of thing - there's something so mysterious about these identities.
My favourite is Euler's identity
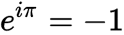
Who'd have believed this? It's freaking magical!
-
THat's good Klaus. You can generalize to k.
Let x be the value of the series with the + signs flipped to - signs at the 1/k^2 term, 1/(2k)^2 term and so on, every kth term. Then calculate pi^2/6 - x .
(pi^2)/6 - x
= 2 * (1/k^2 +1/(2k)^2 + ... )
= (2/k^2)(1 + 1/2^2 + 1/3^2 + ...)
= (2/k^2) * ((pi^2/6))So x = ((pi^2/6)) * (1 - 2/k^2). Done.
Your example:
1 - 1/2^2 + 1/3^2 - 1/4^2 + ...
= (pi^2)/12@jon-nyc said in Puzzle time - Pi squared over six:
THat's good Klaus. You can generalize to k.
Let x be the value of the series with the + signs flipped to - signs at the 1/k^2 term, 1/(2k)^2 term and so on, every kth term. Then calculate pi^2/6 - x .
(pi^2)/6 - x
= 2 * (1/k^2 +1/(2k)^2 + ... )
= (2/k^2)(1 + 1/2^2 + 1/3^2 + ...)
= (2/k^2) * ((pi^2/6))So x = ((pi^2/6)) * (1 - 2/k^2). Done.
Your example:
1 - 1/2^2 + 1/3^2 - 1/4^2 + ...
= (pi^2)/12I don't doubt that the result is correct, but how do you justify the usage of the distributive/commutative/associative laws over an infinite sum? I guess it is correct in this case, but I think it requires an argument as to why it is a valid.
For instance, consider the series 1-1+1-1+1-1+.. . By freely using associativity, you could reason 1-1+1-1+1-1+.. = (1-1) + (1-1) + (1-1) + ... = 0 but also 1-1+1-1+1-1+.. = 1 + (-1+1) + (-1+1) + ... = 1, hence obviously using associativity for this infinite sum isn't valid. The Riemann rearrangement theorem describes another cautionary tale about the invalidity of basic rearrangements when dealing with infinite sums. I guess the absolute convergence of the sum in your example saves the day, but ignoring the issue is dangerous.
-
They were coming at this very differently. In my defense, the question was a little ambiguous.
SOLUTION: Of course, you have no hope of representing a number r unless it's in the closed interval [−pi2/6, pi2/6]. Suppose it is in that interval; then it is natural to try the following "greedy algorithm" to represent it.
If r is positive or zero, start with + 1; otherwise, − 1. At stage n, when you're trying to decide whether to use + 1/n2 or − 1/n2, sum up the fractions you have so far and compare with r. If you've undershot, add 1/n2; otherwise, subtract it.
Does that always work? Alas, no. For example, suppose r = 0.123. Then you will take + 1, but the rest of the terms of the original series only add up to pi2/6 − 1 which is about 0.645, so no amount of subtraction will get you all the way down from 1 to 0.123.
In short, you're stuck if r lies in the open interval (pi2/6 − 2, 2 − pi2/6).
Fortunately, that first term "1" is the only obstruction. The reason is that for any n > 1, the sum of the rest of the series is more than the nth term. Suppose, for example, that you're building up to r and you overshoot with the nth term; then your current error is at most 1/n2, and subtracting terms will eventually get your current sum below r. Since the terms become arbitrarily small, your sum will converge to r.
It follows that the numbers you can get by changing some pluses to minuses are exactly those in the closed interval [−pi2/6, pi2/6 − 2] or the closed interval [2 − pi2/6, pi2/6]. That was a tough one!
[Puzzle inspired by the late Ron Graham's 1964 theorem that a rational number can be expressed as the sum of a finite number of different reciprocals of squares if it lies in between 0 and pi2/6 − 1, or between 1 and pi2/6.]
-
They were coming at this very differently. In my defense, the question was a little ambiguous.
SOLUTION: Of course, you have no hope of representing a number r unless it's in the closed interval [−pi2/6, pi2/6]. Suppose it is in that interval; then it is natural to try the following "greedy algorithm" to represent it.
If r is positive or zero, start with + 1; otherwise, − 1. At stage n, when you're trying to decide whether to use + 1/n2 or − 1/n2, sum up the fractions you have so far and compare with r. If you've undershot, add 1/n2; otherwise, subtract it.
Does that always work? Alas, no. For example, suppose r = 0.123. Then you will take + 1, but the rest of the terms of the original series only add up to pi2/6 − 1 which is about 0.645, so no amount of subtraction will get you all the way down from 1 to 0.123.
In short, you're stuck if r lies in the open interval (pi2/6 − 2, 2 − pi2/6).
Fortunately, that first term "1" is the only obstruction. The reason is that for any n > 1, the sum of the rest of the series is more than the nth term. Suppose, for example, that you're building up to r and you overshoot with the nth term; then your current error is at most 1/n2, and subtracting terms will eventually get your current sum below r. Since the terms become arbitrarily small, your sum will converge to r.
It follows that the numbers you can get by changing some pluses to minuses are exactly those in the closed interval [−pi2/6, pi2/6 − 2] or the closed interval [2 − pi2/6, pi2/6]. That was a tough one!
[Puzzle inspired by the late Ron Graham's 1964 theorem that a rational number can be expressed as the sum of a finite number of different reciprocals of squares if it lies in between 0 and pi2/6 − 1, or between 1 and pi2/6.]
@jon-nyc said in Puzzle time - Pi squared over six:
They were coming at this very differently. In my defense, the question was a little ambiguous.
That makes two in a row. Those nerds need to learn to use the English language to express problems.
-
I did actually briefly think about which numbers one could construct that way, but then thought that that was not was they were after.
But now that they brought it up, I have a follow-up puzzle:
For which class of numbers in the two intervals is the infinite sequence of signs constructible by a finite machine?
For instance, for pi^2 /6, this is obviously possible: The machine just constructs an infinite stream of "+".
But for most numbers that wouldn't be possible: There are uncountably many numbers in the interval but only countably many machines.
