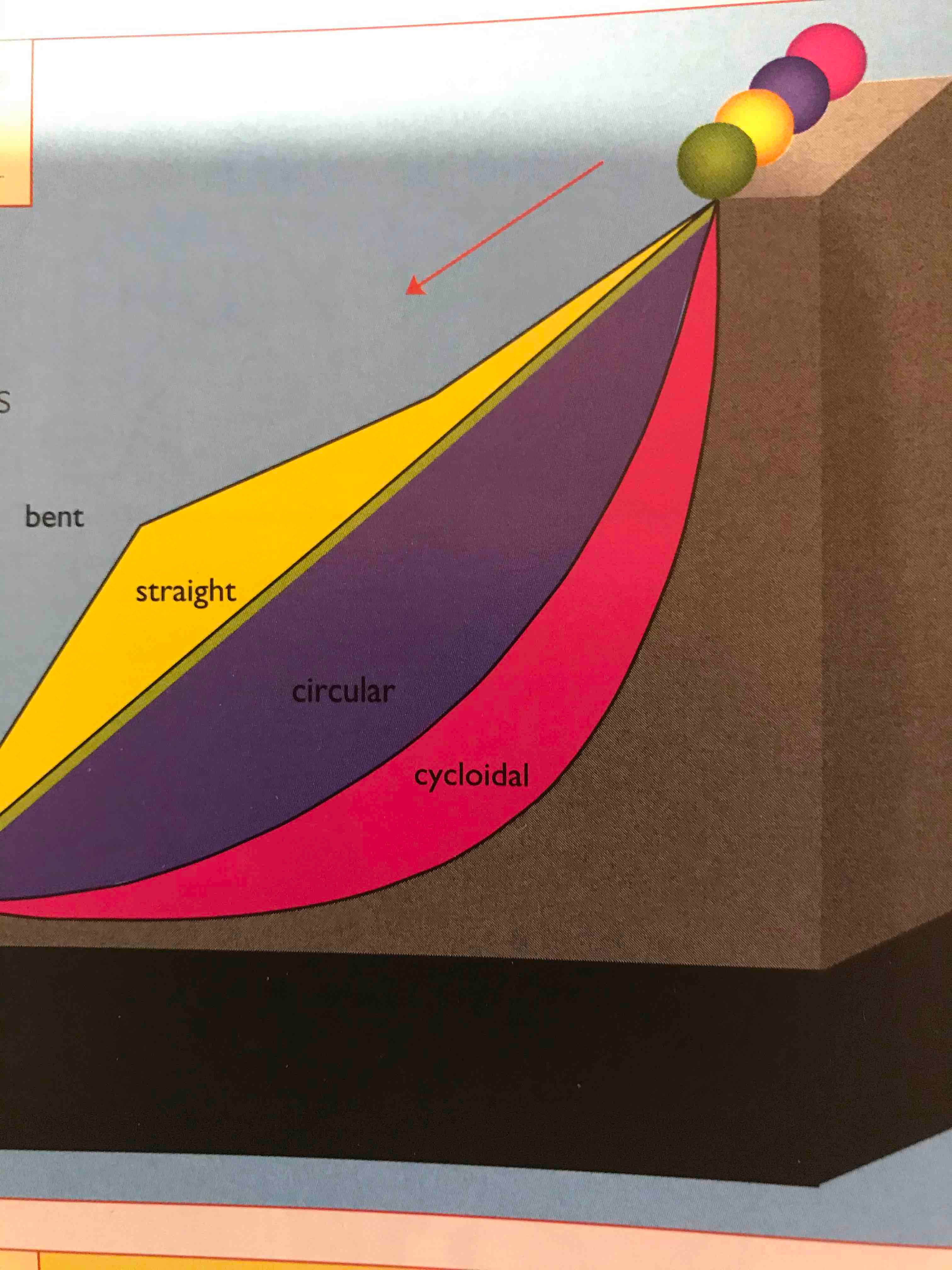
Puzzle Time - Rolling Balls
-
Interesting. I remember very little physics. But the total energy of the balls must stay the same. The initial energy is something like m* g * h if I remember correctly. This gets translated into a mix of rotational energy (how fast the ball rotates) and translational energy (how fast the ball moves). So I'd say the fastest ball is the one that rotates the slowest. I presume that the shortest track - the straight line - yields the slowest rotation, hence I'd go with that one.
My confidence: About 40%.
We are supposed to ignore heat, rolling resistance etc., right?
-
Interesting. I remember very little physics. But the total energy of the balls must stay the same. The initial energy is something like m* g * h if I remember correctly. This gets translated into a mix of rotational energy (how fast the ball rotates) and translational energy (how fast the ball moves). So I'd say the fastest ball is the one that rotates the slowest. I presume that the shortest track - the straight line - yields the slowest rotation, hence I'd go with that one.
My confidence: About 40%.
We are supposed to ignore heat, rolling resistance etc., right?
@Klaus said in Puzzle Time - Rolling Balls:
Interesting. I remember very little physics. But the total energy of the balls must stay the same. The initial energy is something like m* g * h if I remember correctly. This gets translated into a mix of rotational energy (how fast the ball rotates) and translational energy (how fast the ball moves). So I'd say the fastest ball is the one that rotates the slowest. I presume that the shortest track - the straight line - yields the slowest rotation, hence I'd go with that one.
My confidence: About 40%.
We are supposed to ignore heat, rolling resistance etc., right?
Oh, I just see that I misread the question.
You are asking for which ball reaches the end of the slope the fastest. I believe Jon is right about that one. Isn't that a famous historical problem?
I somehow read your post as asking for which track yields the highest terminal speed, and I still guess that the straight line has that property.
-
||Cycloidal. I know enough physics to work out a proof but the fact that high end skate pipes are cycloids tells me someone else already did.||
@jon-nyc said in Puzzle Time - Rolling Balls:
||Cycloidal. I know enough physics to work out a proof but the fact that high end skate pipes are cycloids tells me someone else already did.||
||Same. Acceleration's relationship to movement vectors and time is a thing.||
-
@AndyD @Axtremus @jon-nyc @Aqua-Letifer
Good job guys!!!