Puzzle time - more pie slicing
-
You have a pie slicing machine that chooses two points around the circumference of a pie at random and slices between them. Note both points are randomly chosen, uniformly distributed around the pie.
If your machine makes three cuts, how many pieces would you expect to have?
-
-
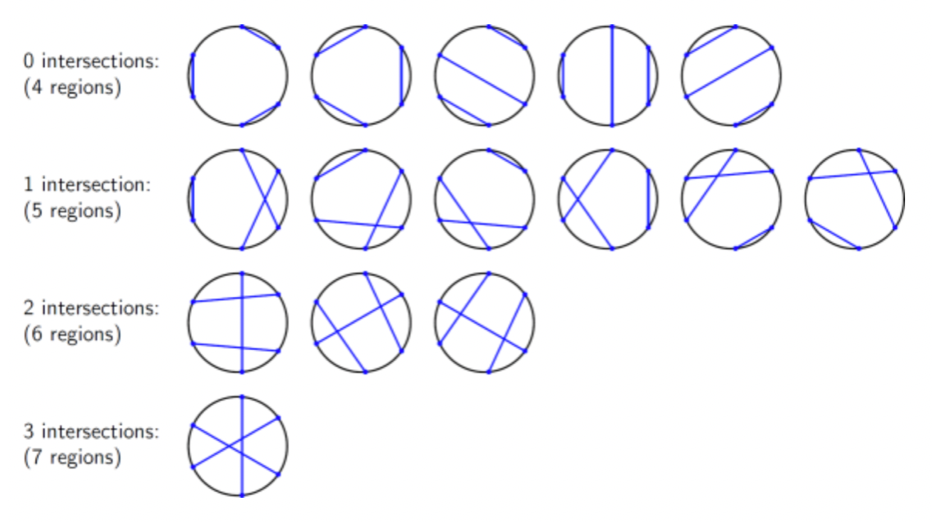
I think that one isn't hard. Choose three pairs of numbers between 0 and 1 (or 0 and 2 pi) at random. Sort them. Interleaving pairs of numbers stand for intersecting lines. All that matters are the number of interleavings. Number of pieces = 4+#interleavings.
-
-
You have a pie slicing machine that chooses two points around the circumference of a pie at random and slices between them. Note both points are randomly chosen, uniformly distributed around the pie.
If your machine makes three cuts, how many pieces would you expect to have?
@jon-nyc said in Puzzle time - more pie slicing:
You have a pie slicing machine that chooses two points around the circumference of a pie at random and slices between them. Note both points are randomly chosen, uniformly distributed around the pie.
If your machine makes three cuts, how many pieces would you expect to have?
Dunno, but my dog's expecting the smallest
-
||Yes. One way to do this is to think of 6 points randomly placed on a circle and consider there are 15 ways to connect them. 5 ways give you 4, 6 ways give you 5, 3 ways get you 6, and one way gets you 7. It averages to 5.
But a general solution is easier. Each new cut adds a piece, plus there’s a 1/3 chance of intersecting each existing cut which also creates a new piece.
So f(1)=2, and, and f(n+1)=f(n)+1+n/3
So the expected number of slices is (n+2)(n+3)/6||
-
||Yes. One way to do this is to think of 6 points randomly placed on a circle and consider there are 15 ways to connect them. 5 ways give you 4, 6 ways give you 5, 3 ways get you 6, and one way gets you 7. It averages to 5.
But a general solution is easier. Each new cut adds a piece, plus there’s a 1/3 chance of intersecting each existing cut which also creates a new piece.
So f(1)=2, and, and f(n+1)=f(n)+1+n/3
So the expected number of slices is (n+2)(n+3)/6||
||
@jon-nyc said in Puzzle time - more pie slicing:Yes. One way to do this is to think of 6 points randomly placed on a circle and consider there are 15 ways to connect them. 5 ways give you 4, 6 ways give you 5, 3 ways get you 6, and one way gets you 7. It averages to 5.
Wait a second, that sounds plausible, but although it gives you the same expected value, the values seem to differ. For instance, your solution gives a probability of 1/15 for 7 pieces, whereas mine gives 1/27. Something's wrong here.
||
-
||
@jon-nyc said in Puzzle time - more pie slicing:Yes. One way to do this is to think of 6 points randomly placed on a circle and consider there are 15 ways to connect them. 5 ways give you 4, 6 ways give you 5, 3 ways get you 6, and one way gets you 7. It averages to 5.
Wait a second, that sounds plausible, but although it gives you the same expected value, the values seem to differ. For instance, your solution gives a probability of 1/15 for 7 pieces, whereas mine gives 1/27. Something's wrong here.
||
-
Seriously there are only 15 distinct ways to connect 6 random points. The lowest probability would be 1 in 15.
@jon-nyc said in Puzzle time - more pie slicing:
Seriously there are only 15 distinct ways to connect 6 random points. The lowest probability would be 1 in 15.
I don't disagree.
But if the probability for two lines to intersect is 1/3, wouldn't the probability for three lines to intersect pairwise be 1/3 * 1/3 * 1/3?
-
I see the oddity. Yet let’s imagine the conditional probability where the first two chords intersect.
When you place the fifth point you have this:
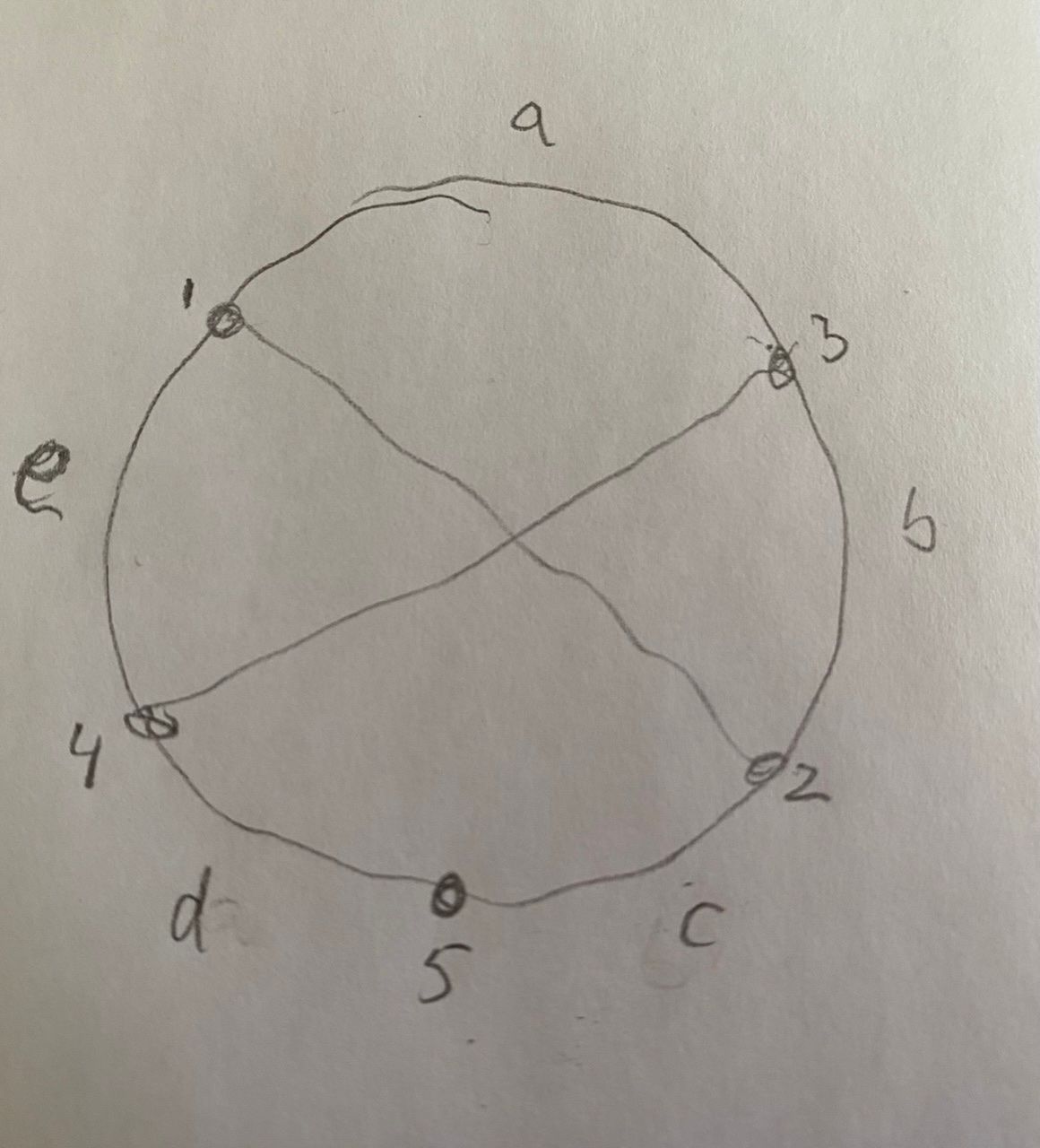
It’s clear that point 6 has an equal chance of being placed in sections a, b, c, d, or e. Only e gives you three intersections. So p = 1/3 * 1/5.