Puzzle time - even sum billiards
-
A box contains nine billiard balls numbered 1 through 9.
You repeat the following ten times: reach blindly into the box, pick out a random ball, note its number, and throw the ball back in the box.
What is the probability that the sum of the numbers of the balls you picked is even?
-
||
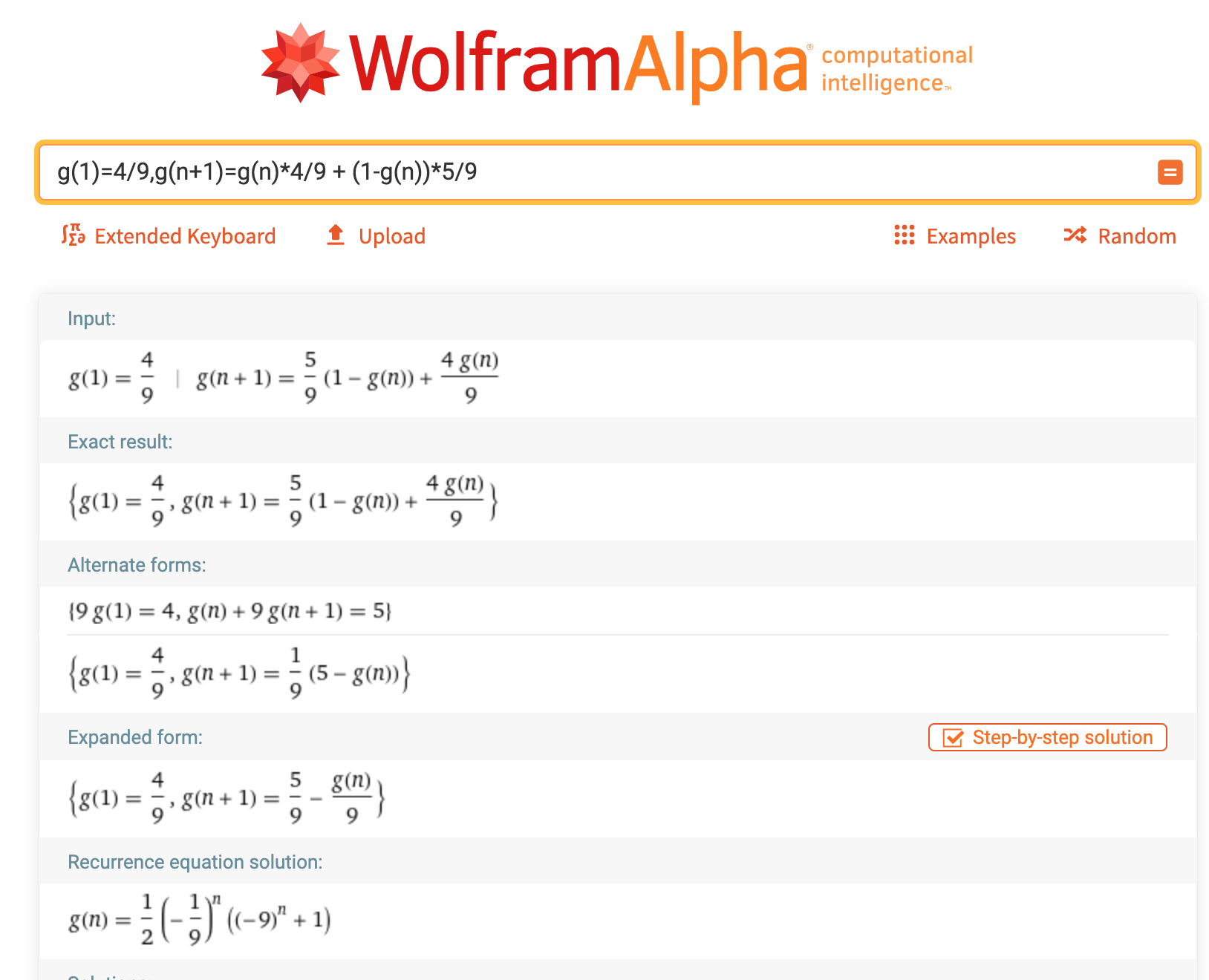
0.5000000001433986Let P(n) denote the probability for even sum after drawing n balls.
Obviously
P(1) = 4/9
and
P(n+1) = P(n)*4/9 + (1-P(n))*5/9(Sum after n+1 draws is even if it was even after n draws and an even number was drawn, or if it was odd and an odd number was drawn)
Computing P(10) gives the result above.
|| -
Hmm, my initial think is that it got to be less than 50%, as there are more oddballs than even balls, but it probably is not right. Lol
( As to oddnumbers equal an even)
-
Yeah but farming it out to Wolfram Alpha makes you miss the interesting point.
The odds after 2 ball draws are :
odd 40/81 vs even: 41/81.
After 3 its:
odd 364/729 vs even: 365/729.
After 4 its:
odd 3280/6561 vs even: 3281/6561.
The pattern is, out of the 9^n possible combinations, the number that sum to even is exactly one more than those that sum to odd.
THat's demonstrable with no math.
Imagine ordering the combinations from 1111111111 to 9999999999 in numerical order.
The first one sums to an even number (10). The next one in the sequence is 1111111112 which is just adding one to the total, hence it's odd.
Straightforwardly, this alternates even-odd-even-odd until you get to 1111111119. But even then, going to the next one in the sequence (1111111121) changes the last digit from 9 back to 1, which makes no change to the even/odd nature of the sum, but the digit in the 10s place increases by one, hence the even/odd sequencing is preserved.
It's easy to convince yourself that this pattern of alternating even/odd will continue all the way up to 9999999999.
But then notice we started at an even number and ended at an even number. Hence one more even combination than odd.
SO the total combinations are 9^n.
The probability of an odd sum are [(9^n-1)/2] / 9^n. And for even it's the same with one added to the numerator.