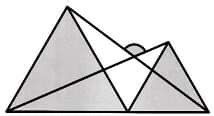
Puzzle time - Find the angle
-
wrote on 14 Oct 2020, 12:53 last edited by jon-nyc
Time for some trig. Find the standalone shaded angle.
And show your reasoning.
-
wrote on 14 Oct 2020, 12:59 last edited by
Found it!
-
wrote on 14 Oct 2020, 13:06 last edited by Doctor Phibes
That's about 115 degrees.
-
wrote on 14 Oct 2020, 13:06 last edited by Klaus
The problem looks underspecified. You'd need to give us some other angles or lengths or areas or whatnot. Are the top left and top right angles 90 degrees? Are the shaded triangles supposed to have the same angles? Are the side length of the shaded triangles all the same, respectively?
-
The problem looks underspecified. You'd need to give us some other angles or lengths or areas or whatnot. Are the top left and top right angles 90 degrees? Are the shaded triangles supposed to have the same angles? Are the side length of the shaded triangles all the same, respectively?
wrote on 14 Oct 2020, 13:57 last edited by@Klaus said in Puzzle time - Find the angle:
The problem looks underspecified. You'd need to give us some other angles or lengths or areas or whatnot. Are the top left and top right angles 90 degrees? Are the shaded triangles supposed to have the same angles? Are the side length of the shaded triangles all the same, respectively?
I agree. Without the little "square" to indicate a 90 degree angle and other numbers, it is impossible to solve (at least I think so!!! LOL)
-
wrote on 14 Oct 2020, 14:11 last edited by
119 degrees.
Here's my reasoning.
||
|| -
wrote on 14 Oct 2020, 14:19 last edited by
-
wrote on 14 Oct 2020, 14:20 last edited by
Sorry - the two shaded triangles are equilateral.
-
wrote on 14 Oct 2020, 14:22 last edited by Klaus
@jon-nyc said in Puzzle time - Find the angle:
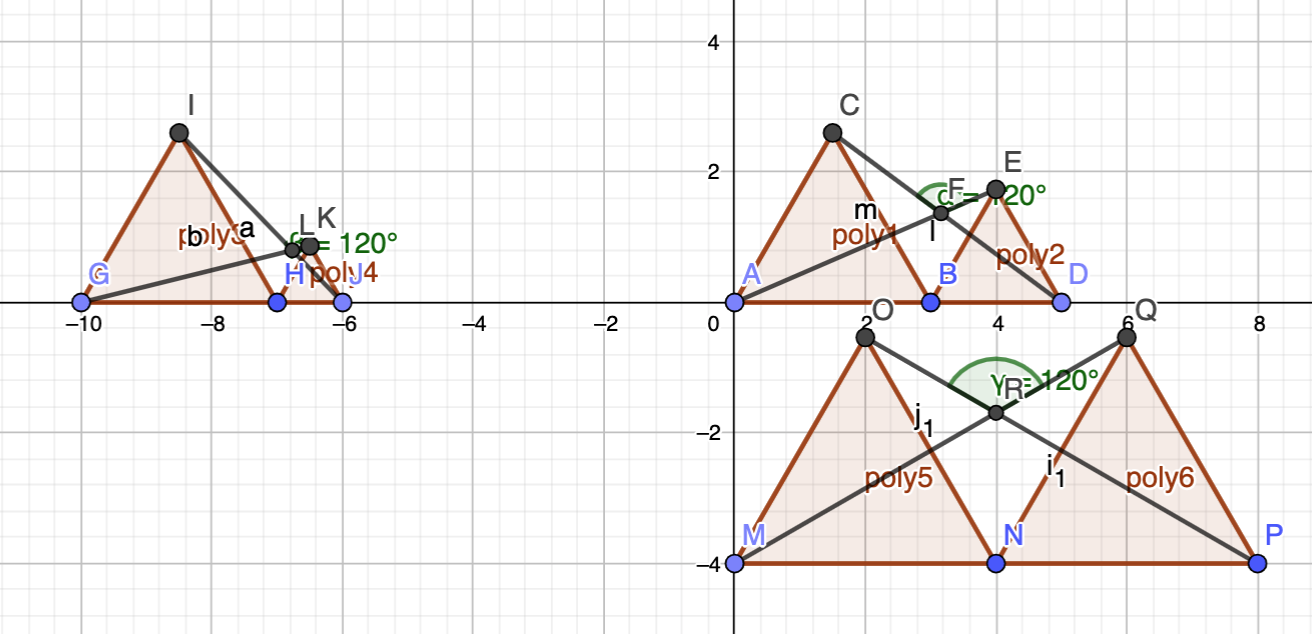
Sorry - the two shaded triangles are equilateral.
But that alone is not enough. For instance, I could shrink one of the triangles by 50% and change the angle. You'd need something else like "the area of the bigger one is twice the area of the smaller".
-
wrote on 14 Oct 2020, 14:24 last edited by
I think I hated trig even more than I hated statistics.
-
wrote on 14 Oct 2020, 14:26 last edited by
How about statistical trigonometry?
-
wrote on 14 Oct 2020, 14:32 last edited by
-
wrote on 14 Oct 2020, 14:57 last edited by
Definitely there is a solution
-
wrote on 14 Oct 2020, 15:01 last edited by
No cheating and saying ‘since it’s true for any relative size triangles let me assume they’re the same size and figure out that special case’.
-
wrote on 14 Oct 2020, 15:23 last edited by
Oh, I see. The relative size doesn't matter. It's always 120 degrees.
-
wrote on 14 Oct 2020, 15:34 last edited by
Can you prove it?
-
wrote on 14 Oct 2020, 15:53 last edited by Klaus
Well, I assume if I set up a formula for the angle given side length a and b for the triangles, then simplify using textbook identities for trigonometric functions, the a's and b's will magically cancel each other all out and I'll just get the 120 degrees.
There should be a tool online that turns geometric constructions into algebraic equations. There's pizza in the oven, so I can't be bothered to do that by hand right now
-
wrote on 14 Oct 2020, 15:56 last edited by
I'm going with 120 degrees.
My reasoning is that Klaus knows about this stuff.
-
wrote on 14 Oct 2020, 15:57 last edited by
Sorry, I should probably have put that in a spoiler
-
wrote on 14 Oct 2020, 16:50 last edited by
You can do it without complex trig identities. In your head in fact.
