Puzzle Time - Car Chase edition
-
You're involved in a car chase, but a very civilized one. You and the pursuer are both following traffic laws and stopping at all red lights.
You're trying to make it to the city limit, and you're currently one block ahead of your pursuer.
You're both stopped at traffic lights, which will turn green at the exact same time. Then you both proceed at a speed of 1 city block per minute.
Every time that you come to an intersection, there’s a 50 percent chance the light is green, in which case you coast right on through. But there’s also a 50 percent chance the light is red, in which case it takes exactly one minute for the light to turn green again. These same probabilities govern the pursuer —at each intersection, he has a 50 percent chance of encountering a green light and a 50 percent chance of encountering a red light and having to wait one minute, entirely independent of whatever you might have encountered at that same intersection.
Including the light at which you are now stopped, there are five traffic lights between you and the city limit, as illustrated below. That means there are six lights for your pursuer.
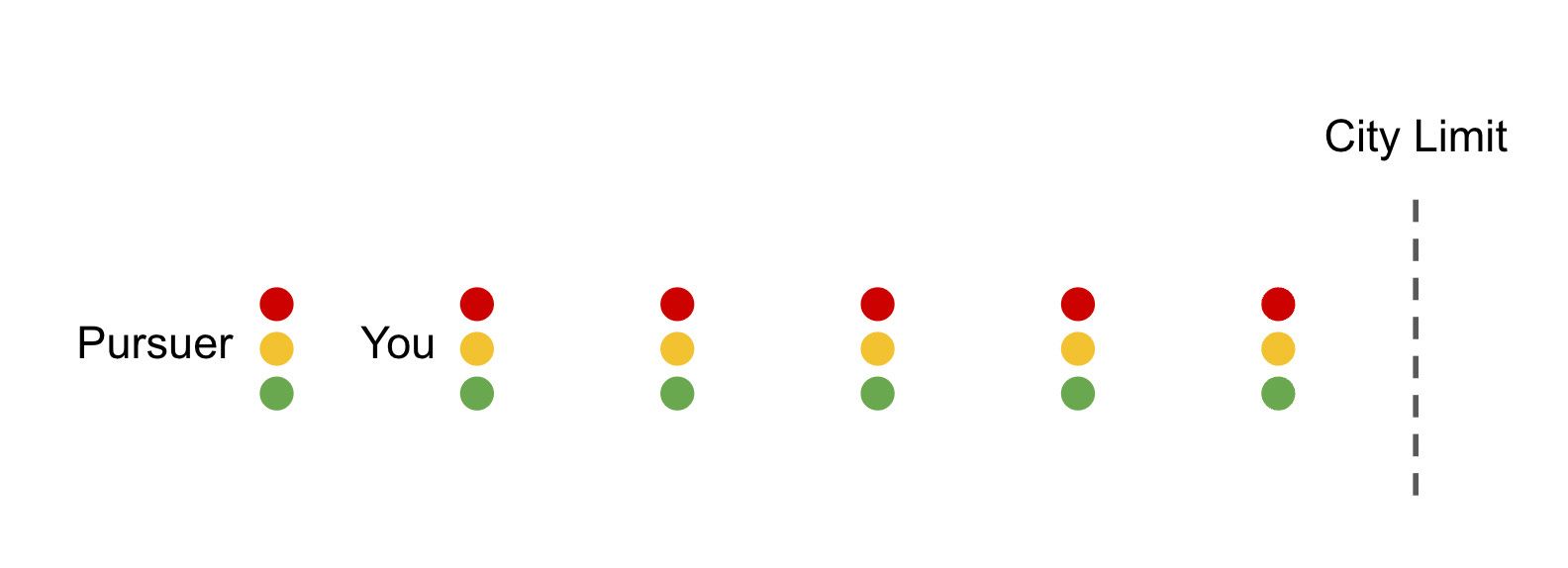
What are the odds you'll make it past the city limit without getting caught?
-
So there’s a random walk where each step is the difference between two random flips of heads or tails, where heads is 0 and tails is 1. The walk starts at -1 and the question is the probability it reaches 0 within six steps. Easy enough to simulate but for closed form formula I’m not sure. 25 percent chance of getting caught at light one, then it gets complicated.
-
The extra credit question is : if the city becomes infinite, what’s the expected number of minutes until you’re caught.
We need closed form for that. Maybe I’ll work on it
@jon-nyc said in Puzzle Time - Car Chase edition:
The extra credit question is : if the city becomes infinite, what’s the expected number of minutes until you’re caught.
We need closed form for that. Maybe I’ll work on it
Does an average make sense when working with unbounded numbers? It makes sense to ask how many steps before you have a > 50% chance of being caught.
-
The official question uses the word average.
You can have unbounded probability distributions with finite means and finite variance, or finite means and infinite variance.
A normal distribution has finite means and variance but is unbounded. A Cauchy distribution is unbounded and has an infinite means and variance (well, ‘undefined’)