Puzzle time - Dots and Frisbees
-
@Horace IOW, what I'm doodling with is a solution that solves for say 8 of the 10 points, and any movement of frisbees that tries to cover all 10 causes overlap.
The above doodles are too spread out -- any such "disproof" would only be concerns with the points around one frisbee -- presumably some one in the center, some on the perimeter, and some in the voids between the hex pattern.
-
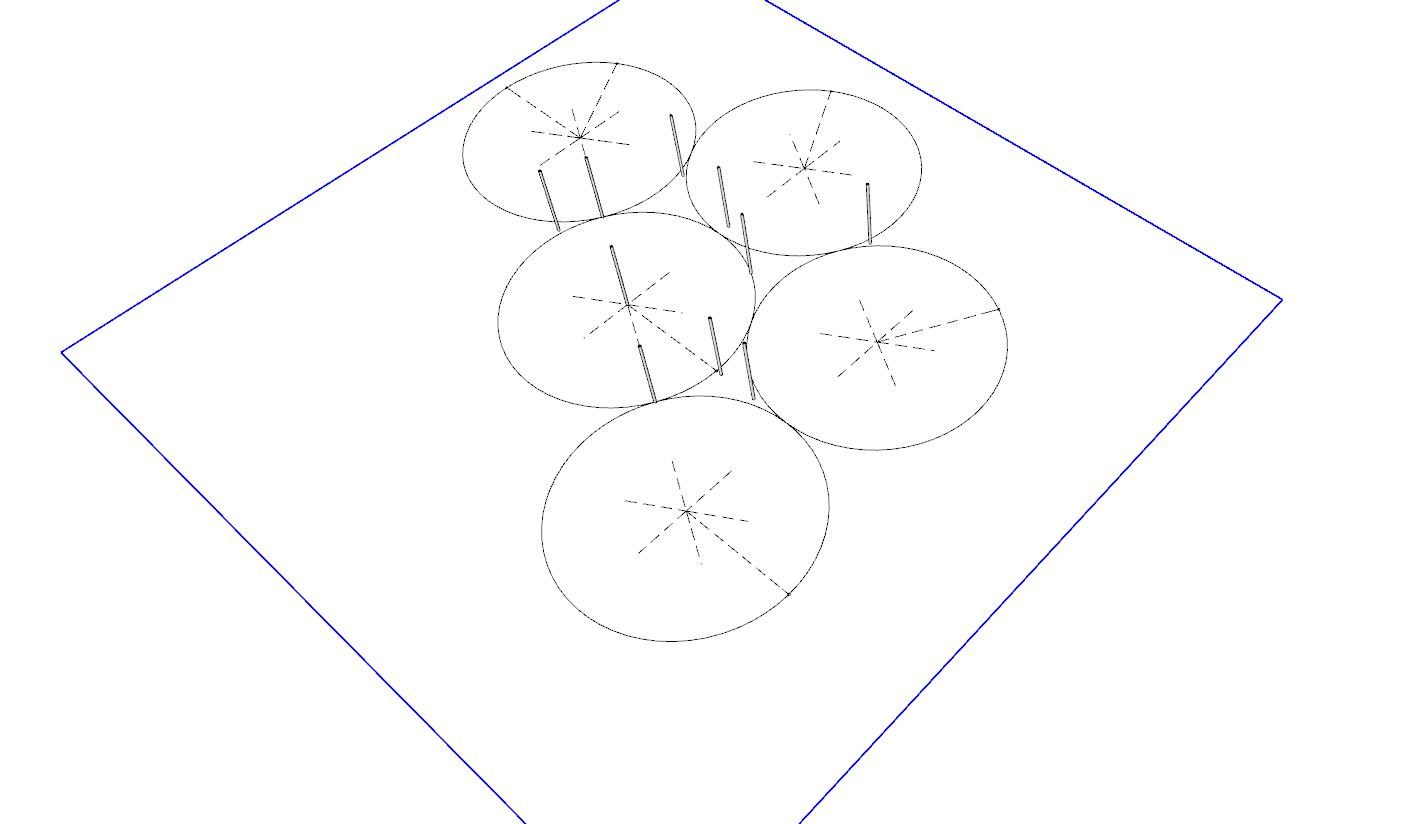
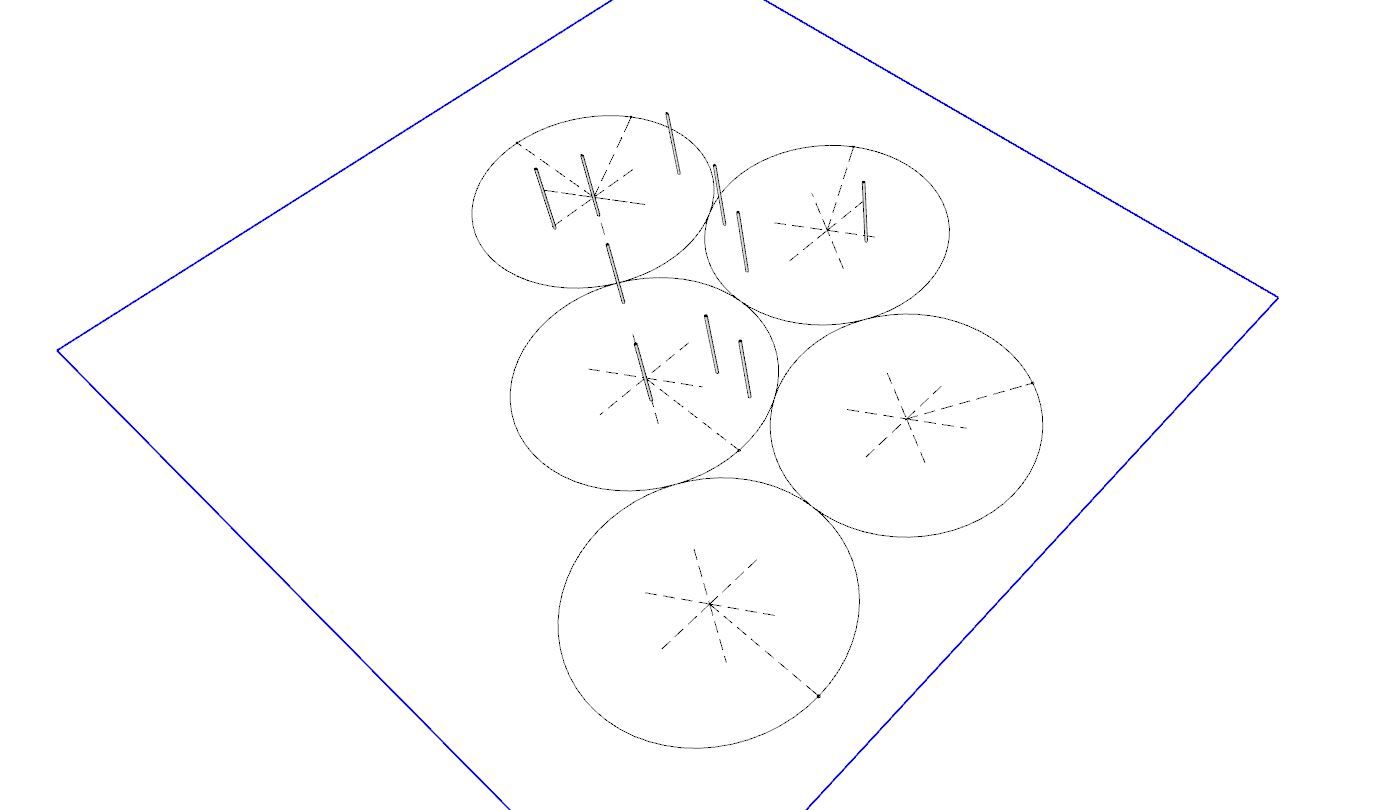
@Horace I must be missing something here, as I'm finding easy solutions.
-
@Ivorythumper said in Puzzle time - Dots and Frisbees:
… I'm finding easy solutions.
My
mathematical cheatseasy solutions:
click to show -
SOLUTION: The naked mathematical question being asked here is: Can any set of 10 dots in the plane be covered by disjoint unit disks? If the dots are close together, you can cover them with one disk; if they're spread widely apart, you can cover each with its own disk. It's the medium distances that could cause problems.
Certainly you can cover any two dots, and a little more thought will convince you that three or four are also doable. How about large numbers of dots?
The answer is certainly "no" if 10 is replaced by 10,000. The reason is that you can't "tile" the plane with unit disks; in other words, you can't arrange disjoint unit disks so as to cover the whole plane (as you could, say, with unit squares). If you put down 10,000 dots in a 100 x 100 grid pattern covering a square somewhat bigger than a unit disk, it won't be possible to cover every dot with disjoint unit disks.
So it's a question of quantity: is 10 more like 3, or more like 10,000? Here's a thought: how much of the plane can be covered by disjoint unit disks? You would probably guess that the best way to pack unit disks is in a hexagonal array, with each row of disks fitted nicely into the cracks between the disks in the row below. And you'd be right.
How good is this disk-packing — in other words, if you choose a large region of the plane (say, a 1,000,000 x 1,000,000 square) and pack it hexagonally with disks, what fraction of the region will be covered? In the limit, that fraction must be the fraction of the area of one of those hexagonal cells that is occupied by an inscribed unit disk. Of course, the disk, if it has radius 1, has area pi. The hexagon is made up of six equilateral triangles of altitude 1 and area 1/sqrt(3), thus total area 6/sqrt(3) = sqrt(12). It follows that the fraction of area covered by the disk is pi/sqrt(12) ~ 0.9069.
Hmm. The disks cover more than 90% of the plane; crudely speaking, more than 9 points out of 10. Can we make use of that? Trouble is, the dots on the floor are not random points, they are (in the worst case) arranged as if by an adversary.
But we can shift the hexagonal disk-packing randomly. To do this, just fix some hexagonal cell and pick a point in it uniformly at random; then shift (without rotating) the whole picture by moving the center of the cell to the selected point. Now we can say that for any dot on the plane, the probability that it is covered by some disk of the randomly shifted configuration is 0.9096.
It follows that of our 10 dots, the average number covered by disks of the randomly shifted hexagonal packing is 9.096. But then some configurations must cover all 10 points, and the problem is solved!
And this is an interesting addition:
[The actual maximum number of points in the plane that can always be covered by disjoint unit disks is not known; embarrassingly, the best results currently are that 12 points are always coverable and 42 are not.]
-
@jon-nyc said in Puzzle time - Dots and Frisbees:
Hmm. The disks cover more than 90% of the plane; crudely speaking, more than 9 points out of 10. Can we make use of that? Trouble is, the dots on the floor are not random points, they are (in the worst case) arranged as if by an adversary.
That's the part I got hung up on. But I understand that this method does work to establish that 10 is always possible. But as puzzles go, this solution seems less than satisfying to me. Probably the same reason you called your solution 'handwavy' even though it's mathematically coherent.
[The actual maximum number of points in the plane that can always be covered by disjoint unit disks is not known; embarrassingly, the best results currently are that 12 points are always coverable and 42 are not.]
Right, that's part of the reason why this solution is not totally satisfying.
-
[The actual maximum number of points in the plane that can always be covered by disjoint unit disks is not known; embarrassingly, the best results currently are that 12 points are always coverable and 42 are not.]
Did they provide any references with regard to those results? I'd like to peek at the proof strategy.
