Puzzle time - Dots and Frisbees
-
That argument would work for a billion dots, would it not?
Yet it is obvious that with enough dots you could sprinkle them in the plane very close to each other, like sand. You can’t push circles close enough to each other to cover all the points as there are biggish gaps between the circles even when you pack them together as closely as possible.
So think of the question as “is there a fiendishly clever way of arranging a mere 10 points that makes a non-overlapping covering by the (say) unit-radius circles impossible?”
-
Yeah, you are right.
I guess one would need to force a frisbee structure like this
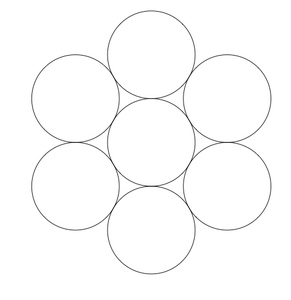
and then put another dot in one of the non-covered areas in between.
Once you have the middle frisbee, forcing the outer ones is simple (add the intersection points, moved by a tiny delta).
But can you force a frisbee to be in a fixed position?
-
Yeah I don’t have an answer yet. I suspect the answer is you can’t guarantee coverage.
Imagine you tile the plane with hexagons and stick the biggest possible circle inside each hexagon, you cover 90.7% of the plane with your circles because that is the ratio of the area of the circle to the area of the hexagon containing it. That is a just over 9 out of 10. Given the problem references 10 points, I’m guessing - just guessing - that that is an inflection point. IOW 9 you can guarantee coverage, 10 you can’t.
-
click to show
-
click to show
@taiwan_girl There’s no requirement that each dot be covered by a distinct frisbee. In your example one frisbee could cover most or all of the dots.
-
@taiwan_girl There’s no requirement that each dot be covered by a distinct frisbee. In your example one frisbee could cover most or all of the dots.
@jon-nyc said in Puzzle time - Dots and Frisbees:
@taiwan_girl There’s no requirement that each dot be covered by a distinct frisbee. In your example one frisbee could cover most or all of the dots.
Okay, so the frisbees can be any size in relation to the dot, but they (frisbees) all have to be the same size.
Hmmmm.
-
I have an answer but it’s a bit hand-wavy.
This hint they gave helped:
HINT: If the frisbees were square, you could cover the whole plane with them, thus most of the floor and all of the dots. You can't do that with disjoint unit disks, but what fraction of the plane can you cover with them?
-
@jon, the smaller the size of the frisbee, the greater "area" of the floor that could have the coverage of the frisbees. As the frisbees get larger, there will be more open area.
-
Ignoring the spaces near the walls (which the problem definition allows us to do) the blank space is the same regardless of the size of the frisbees. Smaller discs have smaller spacing but there are more of them. As Klaus pointed out, you can tile the space completely with hexagons and the biggest circle you can fit in a hexagon covers 90.7% of it, regardless of hexagon size.
-
I have an answer but it’s a bit hand-wavy.
This hint they gave helped:
HINT: If the frisbees were square, you could cover the whole plane with them, thus most of the floor and all of the dots. You can't do that with disjoint unit disks, but what fraction of the plane can you cover with them?
@jon-nyc said in Puzzle time - Dots and Frisbees:
I have an answer but it’s a bit hand-wavy.
This hint they gave helped:
HINT: If the frisbees were square, you could cover the whole plane with them, thus most of the floor and all of the dots. You can't do that with disjoint unit disks, but what fraction of the plane can you cover with them?
A frisbee is circular. Patently so...
-
What's interesting about the proof is that it is non-constructive: You can prove that a covering exists, but the proof doesn't give you a way to actually find that covering. Brouwer and Hilbert fought passionately for decades about whether a non-constructive proof is actually a proof .
-
I'd guess any disproof would require that some points were placed on the circumferences such that rotation or movement of any three, or movement of any two would void the solution.
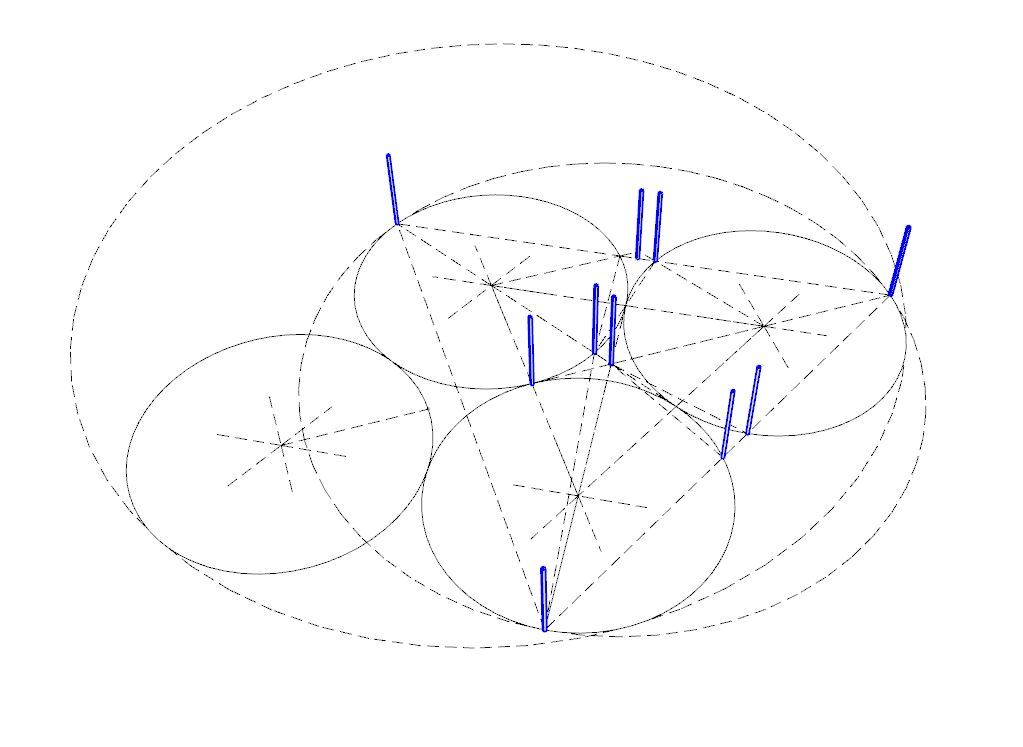
-
I don't see the necessary logical connection between % coverage of the hex pattern of circles, and an intentionally arrayed set of 10 dots meant to avoid coverage.
@Horace said in Puzzle time - Dots and Frisbees:
I don't see the necessary logical connection between % coverage of the hex pattern of circles, and an intentionally arrayed set of 10 dots meant to avoid coverage.
You take an intentionally arrayed set of 10 dots and now consider the expected value of dots covered by a randomly chosen hex covering. If it's >9, there must be a covering with 10.
-
@Horace said in Puzzle time - Dots and Frisbees:
I don't see the necessary logical connection between % coverage of the hex pattern of circles, and an intentionally arrayed set of 10 dots meant to avoid coverage.
You take an intentionally arrayed set of 10 dots and now consider the expected value of dots covered by a randomly chosen hex covering. If it's >9, there must be a covering with 10.
@Klaus said in Puzzle time - Dots and Frisbees:
@Horace said in Puzzle time - Dots and Frisbees:
I don't see the necessary logical connection between % coverage of the hex pattern of circles, and an intentionally arrayed set of 10 dots meant to avoid coverage.
You take an intentionally arrayed set of 10 dots and now consider the expected value of dots covered by a randomly chosen hex covering. If it's >9, there must be a covering with 10.
I'm sure that works. In any case, it's not a disproof that a covering of 11 is always possible. At best, this solution is the simplest one which could establish that 10 is always possible.
-
@Klaus said in Puzzle time - Dots and Frisbees:
@Horace said in Puzzle time - Dots and Frisbees:
I don't see the necessary logical connection between % coverage of the hex pattern of circles, and an intentionally arrayed set of 10 dots meant to avoid coverage.
You take an intentionally arrayed set of 10 dots and now consider the expected value of dots covered by a randomly chosen hex covering. If it's >9, there must be a covering with 10.
I'm sure that works. In any case, it's not a disproof that a covering of 11 is always possible. At best, this solution is the simplest one which could establish that 10 is always possible.
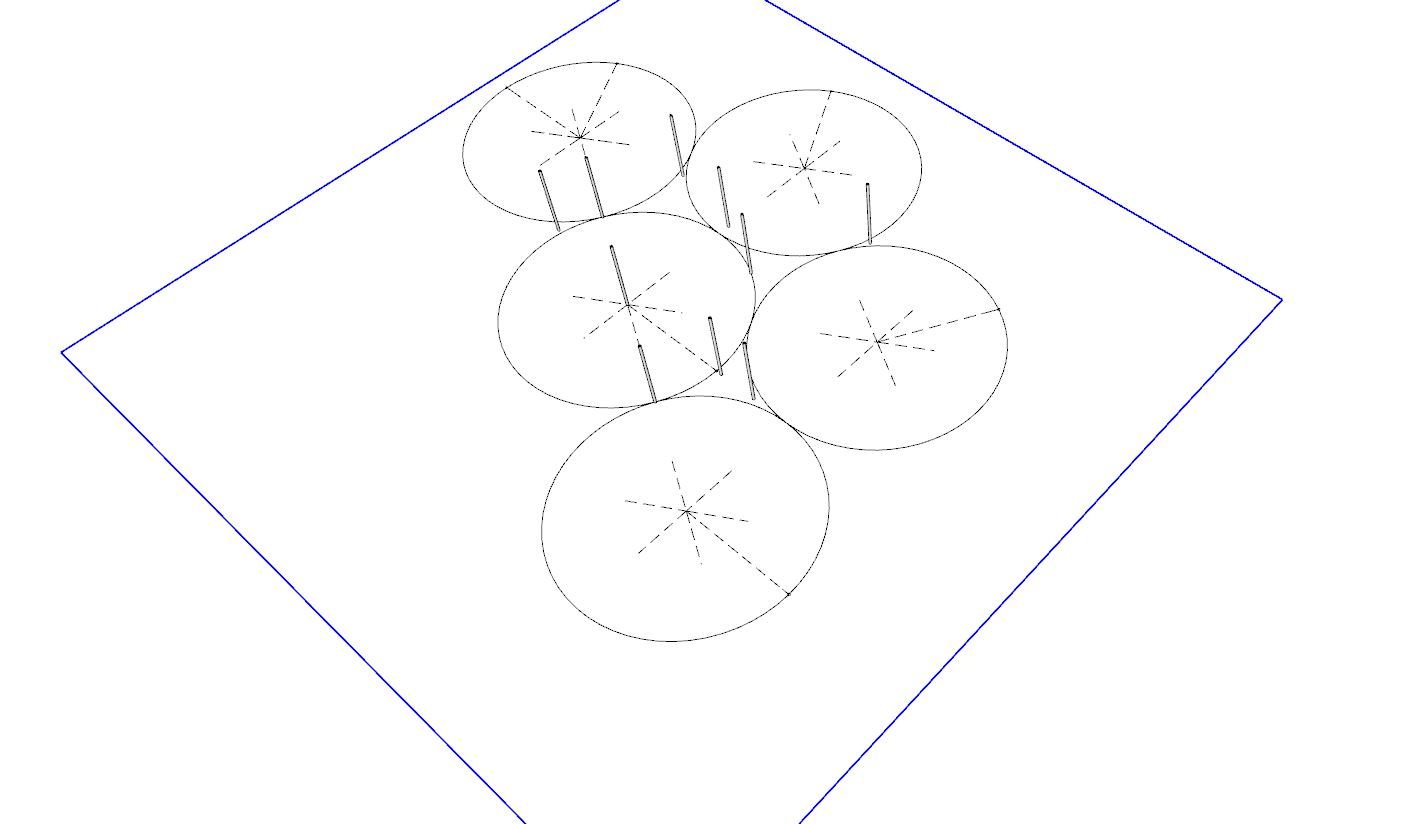
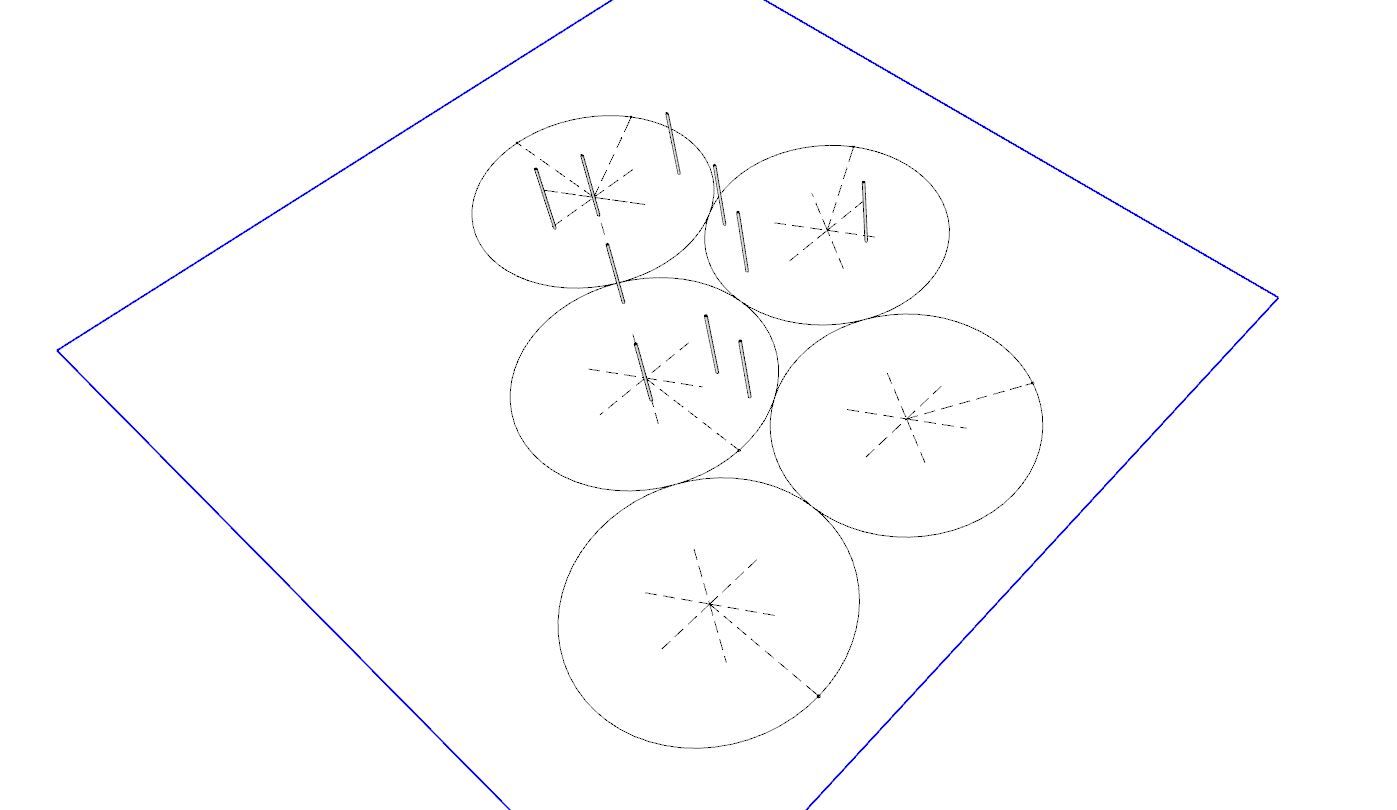
@Horace My drawing shows that 8 of the 10 dots (the blue vertical sticks represent the location of a non-dimensional point) are covered by non-overlapping circles, so 2 are not. The test would be to have any number of non-overlapping circles cover all 10.
I haven't tested any patterns for that yet, but it seems easy enough since the circles don't need to be touching. It doesn't say anything about being in a hex pattern.
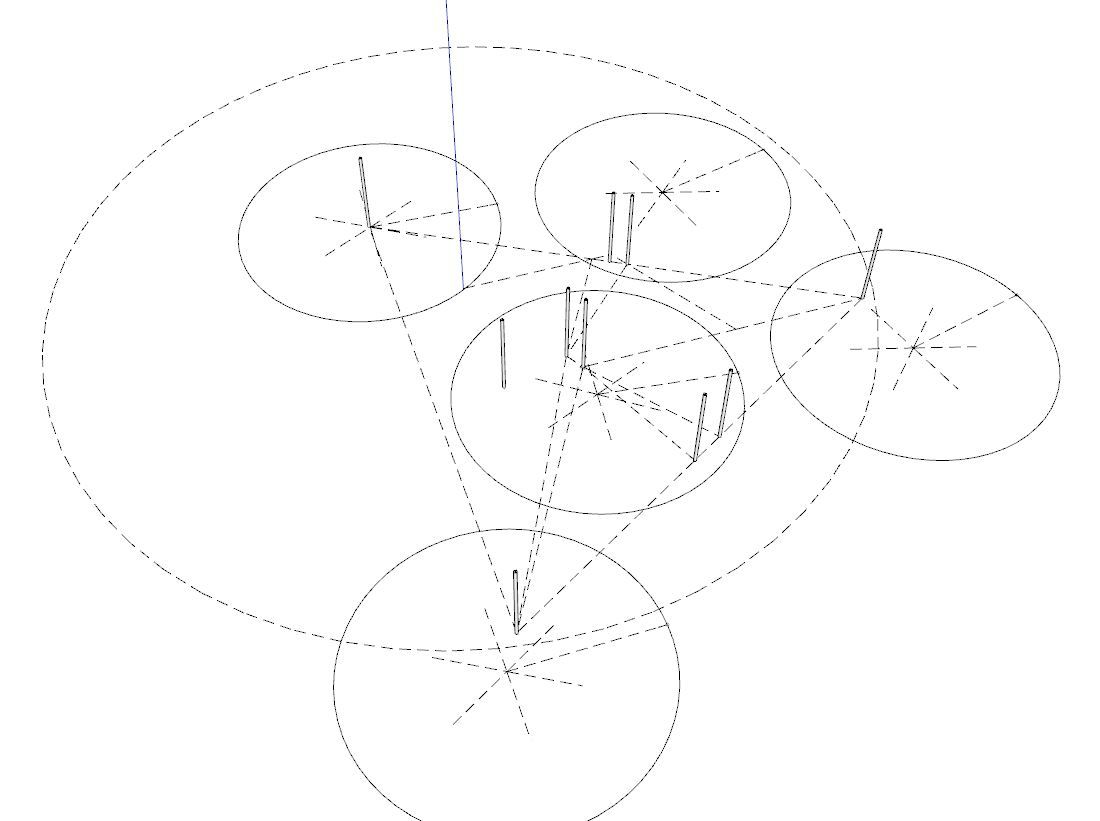
-
@Klaus said in Puzzle time - Dots and Frisbees:
@Horace said in Puzzle time - Dots and Frisbees:
I don't see the necessary logical connection between % coverage of the hex pattern of circles, and an intentionally arrayed set of 10 dots meant to avoid coverage.
You take an intentionally arrayed set of 10 dots and now consider the expected value of dots covered by a randomly chosen hex covering. If it's >9, there must be a covering with 10.
I'm sure that works. In any case, it's not a disproof that a covering of 11 is always possible. At best, this solution is the simplest one which could establish that 10 is always possible.
@Horace IOW, what I'm doodling with is a solution that solves for say 8 of the 10 points, and any movement of frisbees that tries to cover all 10 causes overlap.
The above doodles are too spread out -- any such "disproof" would only be concerns with the points around one frisbee -- presumably some one in the center, some on the perimeter, and some in the voids between the hex pattern.
-
@Klaus said in Puzzle time - Dots and Frisbees:
@Horace said in Puzzle time - Dots and Frisbees:
I don't see the necessary logical connection between % coverage of the hex pattern of circles, and an intentionally arrayed set of 10 dots meant to avoid coverage.
You take an intentionally arrayed set of 10 dots and now consider the expected value of dots covered by a randomly chosen hex covering. If it's >9, there must be a covering with 10.
I'm sure that works. In any case, it's not a disproof that a covering of 11 is always possible. At best, this solution is the simplest one which could establish that 10 is always possible.
@Horace I must be missing something here, as I'm finding easy solutions.