Puzzle Time - Magnetic Dollars
-
I'd say the expected value is 250,000.
Let (a,b) describe the situation with a coins in urn 1 and b coins in urn 2.
The probability for (a,n-a) after round n is 1/(n+1) for any a, i.e., the distribution is uniform.
This sounds almost too simple for a Jon puzzle. Am I missing something?
-
Suppose the proportion of coins in the lesser urn is r after n coins have been tossed. Calculate the expected ratio after the n+1 toss.
This is:
r * (rn+1)/(n+1)
+
(1-r) * (rn/(n+1)= r(n+1)/(n+1)
= r
So the expected ratio never changes. Toss 1, since we start with one coin in each urn, is guaranteed to give us a ratio of 1/3. This expected ratio is the same for any number of tosses. So one third of our million coins are expected to be in the lesser urn.
“Don’t make me repeat myself”
- history
-
I'm not sure that's correct.
Take the situation after two tosses, that is 4 coins:
The probability distribution, unless I miscalculated, is as follows:
(2,2) with p = 0.33
(1,3) with p =0.33
(3,1) with p = 0.33The expected value of the "lesser urn" is
1 x 0.33 + 1 x 0.33 = 0.66 or 16.5%.With five coins in the system, the distribution is:
(1,4) 0.25
(2,3) 0.25
(3,2) 0.25
(4,1),0.25Expected value of lesser urn:
1 x 0.25 + 2 x 0.25 + 2 x 0.25 + 1 x 0.25 = 1.5 or 30%.
After the next toss, we get that every combination has a probability of 0.2, yielding an expected value of 20% for the lesser urn.
The value oscillates around and converges to 25% by the argument in my post above.
-
“Don’t make me repeat myself”
- history
-
@jon-nyc said in Puzzle Time - Magnetic Dollars:
I’m probably overlooking something obvious but how do you get from this:
The probability for (a,n-a) after round n is 1/(n+1) for any a, i.e., the distribution is uniform.
To 250k?
Let's take n = 1,000,000 and consider only the first half of the distribution, i.e., (1, 999.999) to (499.999,500.000), all with equal. Urn 1 is always the one with fewer susans in this half. Let's project on the first component, i.e., the value of urn 1. This is now the uniform distribution unif{1,499.999}. Its mean is (1 + 499.999)/2 = 250.000, see also the last line of the screenshot from the Wikipedia entry on discrete uniform distributions.
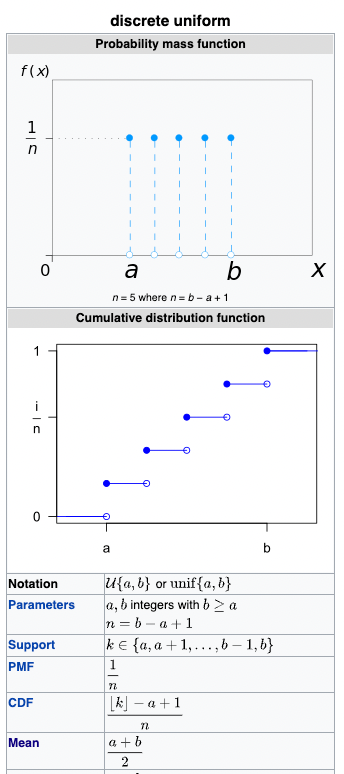
By the same technique we can symmetrically analyze the second half of the distribution, which will also yield a mean of 250.000.
-
“Don’t make me repeat myself”
- history
-
-
Clever proof.
SOLUTION: You might very reasonably worry that one urn will "take over" and leave very little for the other. In my experience, faced with this problem, most people are unwilling to offer $100 in advance for the contents of the lesser urn.
In fact, the lesser urn is worth, on average, a quarter of a million dollars. (Of course, that doesn't mean you are willing to take this much risk!) This is because the final contents of (say) Urn A is precisely equally likely to be any whole number of dollars from $1 all the way to $999,999. Thus, the average amount in the lesser urn is about $250,000.
How can we see this? There are several proofs, but here's my favorite. Imagine that we shuffle a fresh-from-the-box deck of cards in the following careful manner. We place the first card, say the Ace of Spades, face down on the table. Then we take the second card, maybe the Deuce of Spades, and randomly place it over or under the ace. Now there are three possible slots for the Three of Spades; choose one at random, putting it on top of the current pile, under the current pile, or between the ace and deuce, each with probability 1/3.
We continue in this manner; the nth card is inserted in one of n possible slots, each with probability 1/n. The result eventually is a perfectly random permutation of the cards.
Now think of the cards that go in above the Ace of Spades as the coins (not counting the first) that go into Urn A, and the ones that go under as coins going into Urn B. The magnetic rule above describes the process perfectly, because if there are currently x−1 cards above the Ace of Spades (thus x slots) and y−1 cards under the Ace of Spades (thus y slots), the probability that the next card goes above the Ace of Spades is x/(x+y).
Since, in the final shuffled deck, the Ace of Spades is equally likely to be in any position, the number of slots ending up above it is equally likely to be anything from 1 to the number of cards in our deck, which for our puzzle is 999,999.
[Probabilists call the mechanism of this puzzle the Polya urn, after the late George Polya, a Hungarian-born professor at Stanford who famously wrote about problem-solving in mathematics.]
