Puzzle time - Covering numbers

[Klaus]

It's not too hard to google the solution to this one. Give it a try first. It's mind-bending.

An open interval (a,b) is the set of real numbers between a and b excluding a and b itself. The length of (a,b) is the absolute value of a-b.

A covering of a set S of numbers is a set of open intervals such that the union of all the intervals contains S. The length of the covering is the sum of the length of all the open intervals.

We are interested in covering the open set of rational numbers between 0 and 1.

One covering would be the interval (0,1) itself. Its length is 1.

Another covering would be the intervals (0, (sqrt 2)/2) and (sqrt 2)/2,1). It doesn't cover (sqrt 2)/2, but that's an irrational number, so it's still a covering of the rational numbers between 0 and 1. Its length is also 1.

Your task is to find a covering whose length is strictly smaller than 1. Just for fun, let's make this progressively harder. If you post your solution in post number n, then the length of your covering can be at most 1/n.

[Axtremus]

(0,1/4), (3/4,1)

[Klaus]

@axtremus said in Puzzle time - Covering numbers:

(0,1/4), (3/4,1)

That doesn't cover all rational numbers. For instance, 1/2 isn't covered.

[Klaus]

Hint 1: You need to make use of the fact that there are so much fewer rational numbers than real numbers.

Hint 2: Not surprisingly, your covering needs to contain an infinite number of intervals.

[jon-nyc]

The rationals between 0 and 1 are countable; you can write them in order. Put an interval around the first (in your list of rationals) of width 2^(-k-1), the next of width 2^(-k-2), and so on. Their length sum after intersecting each of these intervals with (0,1) is at most 2^(-k). Done.

[Klaus]

@jon-nyc Exactly. You can make the length of the covering as small as you want. It's counter-intuitive, given that there's infinitely many rational numbers between any two real numbers.

The main trick here is how to count the rationals. The most common method goes something like this.

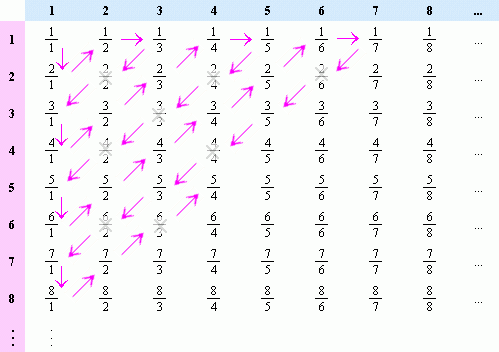
I think this result can also be interpreted as "the amount of rational numbers is negligible compared to the amount of real numbers", which is also true measure-theoretically: If you compute the area covered by the function

f(x) = 1 if x rational and 0 otherwise

then the result is 0.

[jon-nyc]

It’s as counter-intuitive as Zeno’s paradox. There’s an infinite number of rational numbers but they’re covered by increasingly small ranges. Like Zeno needs an infinite number of steps but each gets increasingly smaller.