Puzzle Time - after the decimal point
-
@jon-nyc said in Puzzle Time - after the decimal point:
You can already see the pattern with quite small n.
Yes, but I was confused for a while because that pattern switches when you try larger numbers.
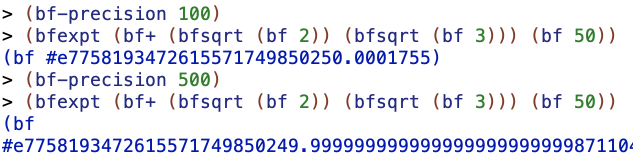
I was at first thinking that this was a rounding error and then tried again with a "big float" library, but still, with n >=50 the first digit seems to be 0.

However, I assume that it's just a particularly numerically unstable formula.
-
@jon-nyc said in Puzzle Time - after the decimal point:
You can already see the pattern with quite small n.

Yes, but I was confused for a while because that pattern switches when you try larger numbers.
I was at first thinking that this was a rounding error and then tried again with a "big float" library, but still, with n >=50 the first digit seems to be 0.

However, I assume that it's just a particularly numerically unstable formula.
-
The ‘official’ answer came out today.
SOLUTION: If you try entering "(sqrt(2) + sqrt(3))^1,000,000,000" into Google or your calculator, you're likely to find that you get only the dozen or so most significant figures; that is, you don't get a nearly accurate enough answer to see what happens after the decimal point.
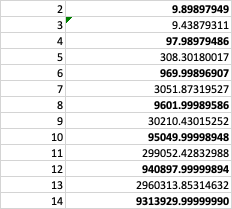
But you can try smaller powers and see what happens. For example, the decimal expansion of the 10th power of the square root of 2 plus the square root of 3 begins 95049.9999895. A bit of experimentation shows that each even power of the square root of 2 plus the square root of 3 seems to be just a hair below some integer. So the solution to the puzzle seems to be 9. But why?
If we merely square the number "square root of 2 plus square root of 3," we get about 9.9. If we play with 10 minus this number, we discover that it's equal to the square of the square root of 2 minus the square root of 3. Aha!
Yes, (sqrt(3) + sqrt(2))^2n + (sqrt(3) - sqrt(2))^2n is always an integer, because when you expand it, the odd-power terms cancel and the even ones are integers. But (sqrt(3) - sqrt(2))^2n is very small, about 10^-n, so the first roughly n digits of (sqrt(3) + sqrt(2))^2n past the decimal point are all 9's.
[The idea for this puzzle comes from the 29th Annual Virginia Tech Mathematics Contest, 2007
 (sqrt3 -sqrt2)^10^9 is too small to influence the first digit after the dot.
(sqrt3 -sqrt2)^10^9 is too small to influence the first digit after the dot.