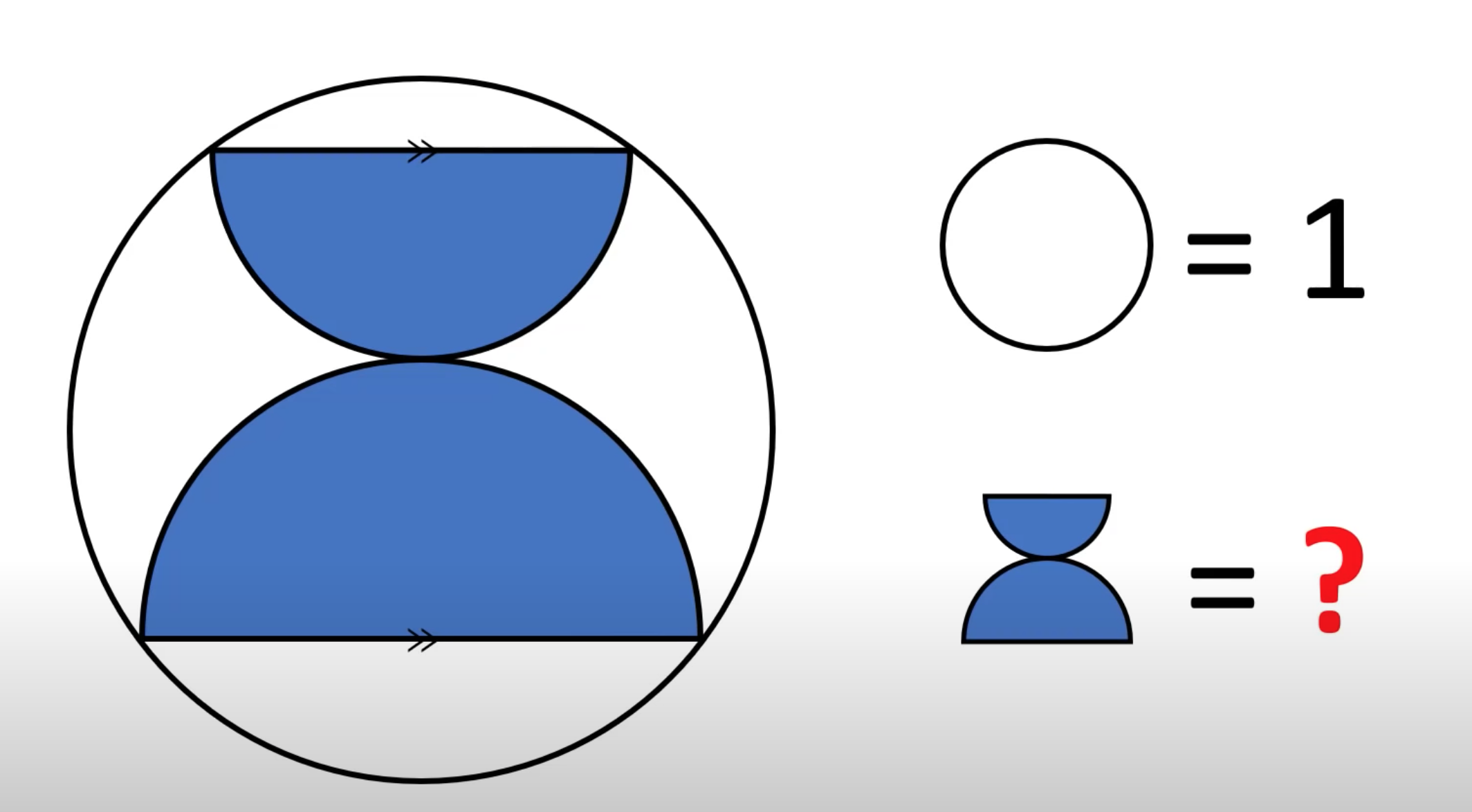
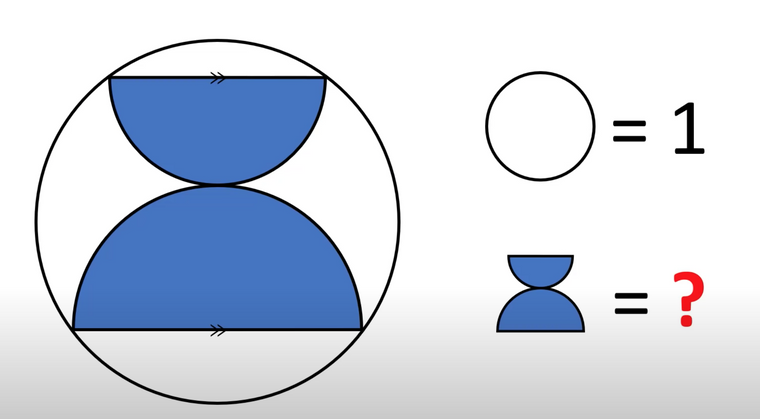
Puzzle time: Geometry
-
:::
1/2.
By questionology i assume it has a single answer, in other words it is invariant as to the size of the two semicircles. Take the limit as one circle grows to the radius of the outer circle and the small circle shrinks to zero.
:::
"You never know what worse luck your bad luck has saved you from."
-Cormac McCarthy -
:::
1/2.
By questionology i assume it has a single answer, in other words it is invariant as to the size of the two semicircles. Take the limit as one circle grows to the radius of the outer circle and the small circle shrinks to zero.
:::
@jon-nyc said in Puzzle time: Geometry:
:::
1/2.
By questionology i assume it has a single answer, in other words it is invariant as to the size of the two semicircles. Take the limit as one circle grows to the radius of the outer circle and the small circle shrinks to zero.
:::
That’s a clever answer. But what’s the mathematical reason for the invariance?
-
:::
1/2.
By questionology i assume it has a single answer, in other words it is invariant as to the size of the two semicircles. Take the limit as one circle grows to the radius of the outer circle and the small circle shrinks to zero.
:::
@jon-nyc I actually guessed this in my mind. No real research, just a guess by trying to "eye" it. LOL
-
Note I'm using the underline to indicate line segment, I don't know how to put an 'overline' across two letter.
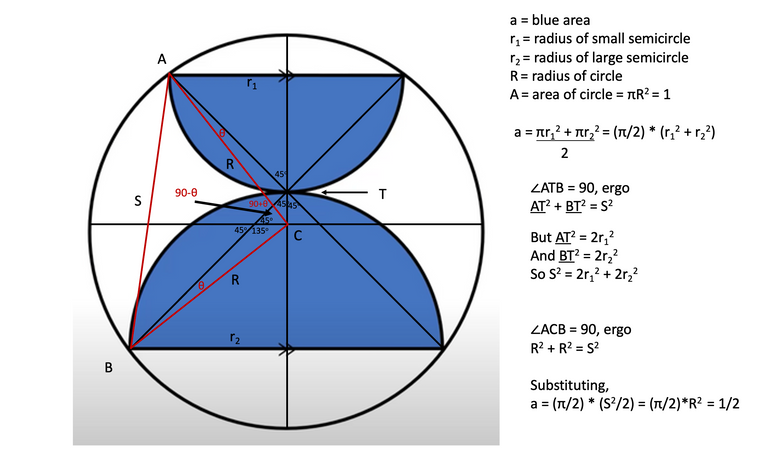
You can picture that red triangle revolving around center point C and the two semicircles would grow and shrink (in opposite directions) from radius R to radius 0.
-
Man you're picky. I marked enough angles that should be obvious.
I have to add some labels so new photo.
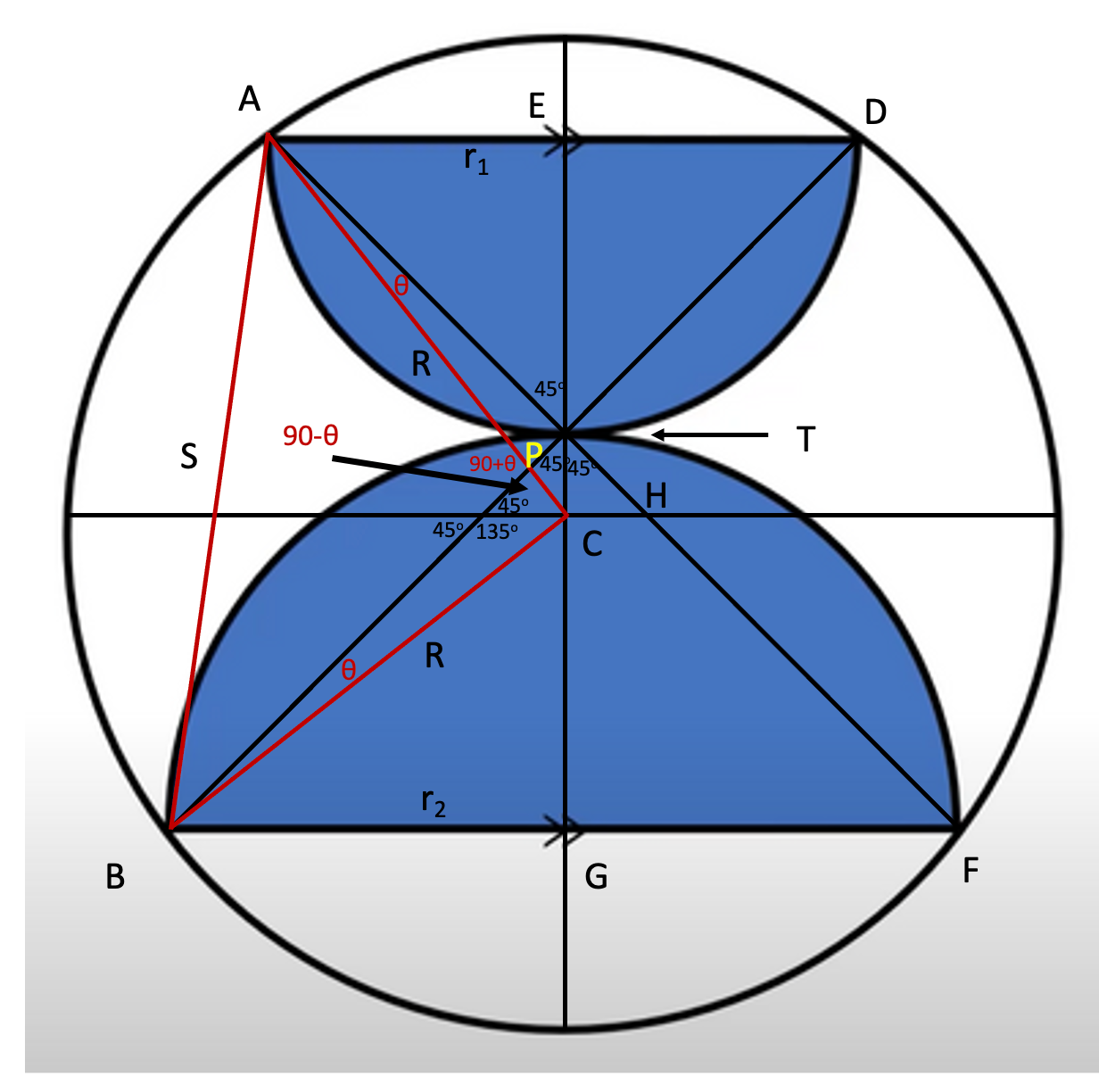
Angle ATD is 90, since ATE and ETD are 45 degrees. That means ATB is 90 since they sum to 180.
It's crowded in there but point P is the intersection touched by the base of the letter itself. Angle PAT I've defined as theta. That means the angle APT is 180 - 90 - theta, or just 90-theta.
That means BPC is also 90-theta.
Angle PBC is theta because triangles ACH and BCP are congruent.
That means ACB is 180 - (90-theta) - theta or 90 degrees.
Bitch. -
Man you're picky. I marked enough angles that should be obvious.
I have to add some labels so new photo.
Angle ATD is 90, since ATE and ETD are 45 degrees. That means ATB is 90 since they sum to 180.
It's crowded in there but point P is the intersection touched by the base of the letter itself. Angle PAT I've defined as theta. That means the angle APT is 180 - 90 - theta, or just 90-theta.
That means BPC is also 90-theta.
Angle PBC is theta because triangles ACH and BCP are congruent.
That means ACB is 180 - (90-theta) - theta or 90 degrees.
Bitch.@jon-nyc said in Puzzle time: Geometry:
Angle ATD is 90, since ATE and ETD are 45 degrees. That means ATB is 90 since they sum to 180.
I think you need to invoke Thales's theorem to argue that ATD is 90.
Angle PBC is theta because triangles ACH and BCP are congruent.
But why are these triangles congruent? It certainly looks like it, but this is again not obvious unless you already assume a part of the solution.
-
Here's a solution that doesn't involve any angles. Radius of upper circle is a and of lower circle is b and of the outer circle r.
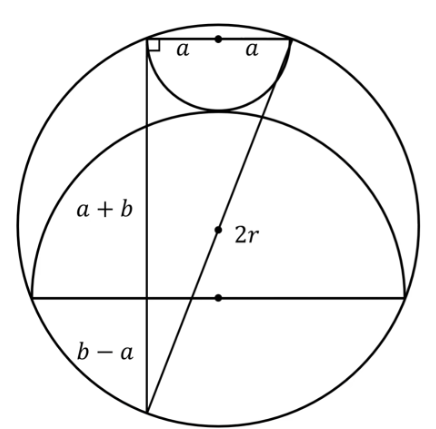
The segment marked with "b-a" has length b-a by the intersecting chords theorem.
Now, by Pythagoras, (2a)^+(2b)^2=(2r)^2, or a^2+b^2=r^2.
The sum of the areas of the semi-circles is 1/2 pi a^2 + 1/2 pi b^2, or pi/2 (a^2+b^2).
Substituting in the equation from above, we get that the combined area is
pi/2 r^2.Since r^2*pi = 1, we get that the area is 1/2.
-
@jon-nyc said in Puzzle time: Geometry:
Angle ATD is 90, since ATE and ETD are 45 degrees. That means ATB is 90 since they sum to 180.
I think you need to invoke Thales's theorem to argue that ATD is 90.
Angle PBC is theta because triangles ACH and BCP are congruent.
But why are these triangles congruent? It certainly looks like it, but this is again not obvious unless you already assume a part of the solution.
@klaus said in Puzzle time: Geometry:
@jon-nyc said in Puzzle time: Geometry:
Angle ATD is 90, since ATE and ETD are 45 degrees. That means ATB is 90 since they sum to 180.
I think you need to invoke Thales's theorem to argue that ATD is 90.
Not necessary. Angle ATE and Angle DTE being 45º each is easy to derive from the observation that Angle AET and Angle DET are 90º each. Add up Angle ATE and Angle DTE you get 90º for Angle ATD.
-
Here's a solution that doesn't involve any angles. Radius of upper circle is a and of lower circle is b and of the outer circle r.
The segment marked with "b-a" has length b-a by the intersecting chords theorem.
Now, by Pythagoras, (2a)^+(2b)^2=(2r)^2, or a^2+b^2=r^2.
The sum of the areas of the semi-circles is 1/2 pi a^2 + 1/2 pi b^2, or pi/2 (a^2+b^2).
Substituting in the equation from above, we get that the combined area is
pi/2 r^2.Since r^2*pi = 1, we get that the area is 1/2.
@klaus said in Puzzle time: Geometry:
Here's a solution that doesn't involve any angles. Radius of upper circle is a and of lower circle is b and of the outer circle r.
The segment marked with "b-a" has length b-a by the intersecting chords theorem.
Now, by Pythagoras, (2a)^+(2b)^2=(2r)^2, or a^2+b^2=r^2.
The sum of the areas of the semi-circles is 1/2 pi a^2 + 1/2 pi b^2, or pi/2 (a^2+b^2).
Substituting in the equation from above, we get that the combined area is
pi/2 r^2.Since r^2*pi = 1, we get that the area is 1/2.
Yeap, that's the solution that requires Thales theorem for you to establish that the "hypothenuse" has to cut through the middle of the circle and thus has the length 2r. Without this you would not be able to relate "r" to "a" and 'b".
