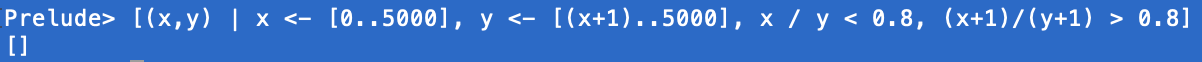Puzzle time - penalty kicks
-
I think yes, but haven’t really thought about the math.
Just ran some numbers in my head.
-
@jon-nyc said in Puzzle time - penalty kicks:
penalty kick percentage
How is "penalty kick percentage" defined?
The # of penalty kicks that result in a goal divided by # of penalty kicks attempted, is that right? -
:::
Proof by counter example:
Start of year the footballer’s penalty kick percentage was 79/99*100%, so just a bit under 80%.
In that year, the footballer attempted only one penalty kick and that penalty kick scored a goal, so at the end of the year his pernalty kick percentage became 80/99*100%, a bit over 80%.
The footballer went from just a bit below 80% to just about over 80% without ever dwelling at exactly 80%. So there need not be a time when it was at exactly 80%.
:::
-
:::
Proof by counter example:
Start of year the footballer’s penalty kick percentage was 79/99*100%, so just a bit under 80%.
In that year, the footballer attempted only one penalty kick and that penalty kick scored a goal, so at the end of the year his pernalty kick percentage became 80/99*100%, a bit over 80%.
The footballer went from just a bit below 80% to just about over 80% without ever dwelling at exactly 80%. So there need not be a time when it was at exactly 80%.
:::
-
-
-
Lets do some arithmetic. We're looking for an 'a' and 'b' such that:
a/b<4/5
(a+1)/(b+1)>4/5The first equation simplifies to:
5a<4bThe second simplifies to:
5a+1>4b.So 5a+1 > 4b > 5a.
But that can't be true for positive integers a and b. So the answer is you can't skip 80%.
Ax notices some other numbers you can't skip. He noticed that 90%, 50% have the same property.
Can you generalize the property?
-
Lets do some arithmetic. We're looking for an 'a' and 'b' such that:
a/b<4/5
(a+1)/(b+1)>4/5The first equation simplifies to:
5a<4bThe second simplifies to:
5a+1>4b.So 5a+1 > 4b > 5a.
But that can't be true for positive integers a and b. So the answer is you can't skip 80%.
Ax notices some other numbers you can't skip. He noticed that 90%, 50% have the same property.
Can you generalize the property?
@jon-nyc said in Puzzle time - penalty kicks:
Can you generalize the property?
Yes, if you divide two integers (with the numerator smaller than the denominator) and you continually increase both by 1, you will eventually have the answer equal 0.5, 0.8, and 0.9!!
5555
-
:::
Let's see ...
From:
a/b < A/B AND (a+1)/(b+1) > A/BWe get to Ba + (B-A) > Ab > B*a
If we are talking only natural numbers, the condition boils down to (B-A) = 1.
So fractions like 1/2 (50%), 2/3 (66.666...%), 3/4 (75%), 4/5 (80%), ... 9/10 (90%) ... all fractions that can be written as X/(X+1) are "special" that way.
:::
-
@axtremus said in Puzzle time - penalty kicks:
FWWI, @Klaus might be happy to know that this puzzle got me to install Haskell.

There are infinitely many good reasons to install Haskell, but if all you want is list comprehensions, then you can do the same thing in many other languages, such as Python.

In Haskell you can of course write the program in a cooler and more general way using monads.
import Control.Monad [1..500] >>= \x -> [1..500] >>= \y -> guard (x/y < 0.8 && (x+1)/(y+1) > 0.8) >> return (x,y) -
I have read @Klaus mentioning Haskell a few times in the past, and has been meaning to check it out. This puzzle is just the thing that finally got me to do. These days my primary computer programming language seems to be “go” (or “golang”), mostly because I found it quite convenient for dealing with web APIs.