Puzzle time - two integers
-
Of two unknown integers between 2 and 99, Leibniz is told the product and Newton is told the sum.
The following conversation happens.
Leibniz: “I don’t know the numbers.
Newton: “I knew that.”
Leibniz: “If that’s the case then I do know them.”
Newton: “If that’s the case, so do I.”
What are the two numbers? Prove your solution is unique.
-
Could you change the story such that Leibniz "wins" in some meaningful way in the end?
In the English-speaking world, Newton is always celebrated as the inventor of calculus, although Leibniz' contributions were more significant and influential. He deserves to kick Newton's ass.
-
Could you change the story such that Leibniz "wins" in some meaningful way in the end?
In the English-speaking world, Newton is always celebrated as the inventor of calculus, although Leibniz' contributions were more significant and influential. He deserves to kick Newton's ass.
@klaus Is this better?
Leibniz: “I don’t know the numbers.
Newton: “I knew that.”
Leibniz: “If even you knew that, then I definitely know them. Bitch.”
Newton: “If that’s the case, so do I.”
Leibniz: “So we both have intimate knowledge of them. Like your fucking sister”.
-
||2 and 3
Had it been 2 and 2, both men would know immediately as both would be told 4 as the product and the sum.
They had to go through one round of them “don’t knowing” to rule out 2 and 2.
The answers are “small enough” such that immediately in the the next round, one guy “knows” right after ruling out 2 and 2. That leaves 2 and 3.
|| -
||2 and 3
Had it been 2 and 2, both men would know immediately as both would be told 4 as the product and the sum.
They had to go through one round of them “don’t knowing” to rule out 2 and 2.
The answers are “small enough” such that immediately in the the next round, one guy “knows” right after ruling out 2 and 2. That leaves 2 and 3.
|| -
@jon-nyc said in Puzzle time - two integers:
With those numbers Newton would have known from the sum alone.
||OK, 3 and 4 then.
No ambiguity with 3 and 3.
But enough ambiguity with 3 and 4.|| -
Why not approach it this way:
What are the implications of statement 1 by itself? How does statement 2 further constrain the possible answers? Etc.
This is definitely easier than trying pairs and seeing if the conversation rules them out.
-
I assume you can reason about prime factor decompositions. For instance, if (and only if) the product decomposes into two prime numbers, or if one of the prime factors is > 50, then the product determines the two factors. I assume similar arguments can be made about the other statements such that the two numbers can eventually be derived analytically.
Too lazy to do that now, though. Never think if you can let the computer do the work

-
Something like this?
All possible sums leading to Newton’s number consist of two numbers leading to a product that has at least two solutions under the given conditions (otherwise he can’t be sure that Leibniz does not know the 2 numbers). If the possible numbers leading to Leibniz’ product have only one such possible combination for the sum, then Newton’s remark leads to Leibniz knowing the numbers.If that’s correct, just give me a year or 50 to figure out the math formula to find the solution

-
Yes, @Nunatax that's spot on.
First lets look at what we learn by each statement.
From the first statement, (Leibniz saying he doesn't know x and y from P) we can infer that P isn't the product of 2 primes, and that it isn't the product a a prime above 50 and another number.
From the second statement (Newton saying he knew Leibniz wouldn't know), we can infer that the sum is a number that cannot be expressed as the sum of two primes. Due to Goldbach's conjecture, we eliminate all of the positive numbers as potential sums, and any odd number that can be expressed as 'prime + 2'.
This leaves us with the set I'll call S0 (that’s S zero):
S0 = {11,17,23,27,29,35,37,41,47,51,53}
Now the third statement, Leibniz knows the answer. That means the product P can only be factored into a single pair x,y such that x+y is an element of S0. For example, the product isn't 30, because both (2,15) and (6,5) sum to elements of S0. But the product could be (say) 18, because of the possible factor pairs (2,9), (3,6) only one of them sums to a member of S0. I'll need shorthand for this below, so let's call a product 'decidable by Leibniz' if it has this property.
Now the 4th statement. Newton says "Now that I've know you know the answer, I know it, too". This means that, of all the (qualifying - ie between 2-99) pairs x,y that sum to S, only one of them is 'decidable by Leibniz'.
So here you might think you need to look at every possible (qualifying) pair that sums to one of those 11 numbers in S0, find it's product, and see whether it is 'decidable by Leibniz', and then track which element in S0 has only one such pair. Lots of work.
But there's a clever shortcut that lets us eliminate most of the elements of S0.
Any element of S0 that can be expressed in multiple ways as a prime number + a multiple of 2 is automatically ruled out. Why? Remember that every element of S0 is odd, so any pair x,y must contain an even and an odd number. But if a number is (prime + multiple of 2) there's only one way to express it as the product of an even and odd number. So necessarily it can't have 2 factor pairs that sum to an element of S0, so it is what we called above 'decidable by Leibniz'. If an element of S0 can be expressed in multiple ways as (prime+multiple of 2) then it is it has multiple pairs 'decidable by Leibniz' and therefor cannot be 'decidable by Newton' in the last step of the conversation.
We can therefore rule out the following:
11 (as it equals 4+7 and 8+3)
23 (as it equals 4+19 and 16+7)
27 (as it equals 4+23 and 8+19)
35 (as it equals 4+31 and 16+19)
37 (as it equals 8+29 and 32+5)
47 (as it equals 4+43 and 16+31)
51 (as it equals 4+47 and 8+43)Which leaves us with S1={17, 29, 41, 53}
Ok, now we have to do some calculations. Start with 17. It has 7 qualifying pairs that sum to it. We'll look at each and see if the pair would be 'decidable by Leibniz':
2,15 not decideable by Leibniz, because 6 * 5 also 30 and also sums to an element of S0 (11)
3,14 not decideable by Leibniz, because 2 * 21 also 42 and also sums to an element of S0 (23)
4,13 decideable by Leibniz
5,12 not decideable by Leibniz, because 3 * 20 also 60 and also sums to an element of S0 (23)
6,11 not decideable by Leibniz, because 2 * 33 also 66 and also sums to an element of S0 (35)
7,10 not decideable by Leibniz, because 2 * 35 also 70 and also sums to an element of S0 (37)
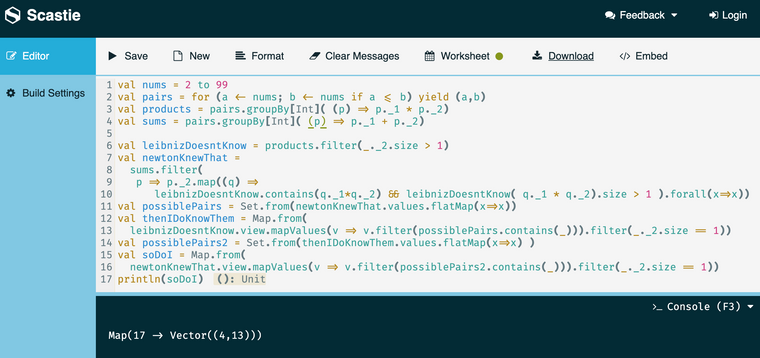
8,9 not decideable by Leibniz, because 3 * 24 also 72 and also sums to an element of S0 (27)So we have an answer. x,y = (4,13)
Is it unique? You might think we have to do the same exercise we just did for 17 with 29, 41, and 53 which have far more pairs and therefore would be far more tedious. But you don't need to look at all pairs, just find 2 that are 'decidable by Leibniz'. Remember we already have a shortcut to finding one that is 'decidable by Leibniz', namely a prime + a multiple of 2. We only need to poke around to find one more.
If you do that you get (one possible answer anyway):
29: (16, 13) and (4,25) are both 'decidable by Leibniz'
41: (4,37) and (3,38) are both 'decidable by Leibniz'
53: (6,47) and (16,37) are both 'decidable by Leibniz'So our original answer pair 4,13 is unique.
-
Yes, @Nunatax that's spot on.
First lets look at what we learn by each statement.
From the first statement, (Leibniz saying he doesn't know x and y from P) we can infer that P isn't the product of 2 primes, and that it isn't the product a a prime above 50 and another number.
From the second statement (Newton saying he knew Leibniz wouldn't know), we can infer that the sum is a number that cannot be expressed as the sum of two primes. Due to Goldbach's conjecture, we eliminate all of the positive numbers as potential sums, and any odd number that can be expressed as 'prime + 2'.
This leaves us with the set I'll call S0 (that’s S zero):
S0 = {11,17,23,27,29,35,37,41,47,51,53}
Now the third statement, Leibniz knows the answer. That means the product P can only be factored into a single pair x,y such that x+y is an element of S0. For example, the product isn't 30, because both (2,15) and (6,5) sum to elements of S0. But the product could be (say) 18, because of the possible factor pairs (2,9), (3,6) only one of them sums to a member of S0. I'll need shorthand for this below, so let's call a product 'decidable by Leibniz' if it has this property.
Now the 4th statement. Newton says "Now that I've know you know the answer, I know it, too". This means that, of all the (qualifying - ie between 2-99) pairs x,y that sum to S, only one of them is 'decidable by Leibniz'.
So here you might think you need to look at every possible (qualifying) pair that sums to one of those 11 numbers in S0, find it's product, and see whether it is 'decidable by Leibniz', and then track which element in S0 has only one such pair. Lots of work.
But there's a clever shortcut that lets us eliminate most of the elements of S0.
Any element of S0 that can be expressed in multiple ways as a prime number + a multiple of 2 is automatically ruled out. Why? Remember that every element of S0 is odd, so any pair x,y must contain an even and an odd number. But if a number is (prime + multiple of 2) there's only one way to express it as the product of an even and odd number. So necessarily it can't have 2 factor pairs that sum to an element of S0, so it is what we called above 'decidable by Leibniz'. If an element of S0 can be expressed in multiple ways as (prime+multiple of 2) then it is it has multiple pairs 'decidable by Leibniz' and therefor cannot be 'decidable by Newton' in the last step of the conversation.
We can therefore rule out the following:
11 (as it equals 4+7 and 8+3)
23 (as it equals 4+19 and 16+7)
27 (as it equals 4+23 and 8+19)
35 (as it equals 4+31 and 16+19)
37 (as it equals 8+29 and 32+5)
47 (as it equals 4+43 and 16+31)
51 (as it equals 4+47 and 8+43)Which leaves us with S1={17, 29, 41, 53}
Ok, now we have to do some calculations. Start with 17. It has 7 qualifying pairs that sum to it. We'll look at each and see if the pair would be 'decidable by Leibniz':
2,15 not decideable by Leibniz, because 6 * 5 also 30 and also sums to an element of S0 (11)
3,14 not decideable by Leibniz, because 2 * 21 also 42 and also sums to an element of S0 (23)
4,13 decideable by Leibniz
5,12 not decideable by Leibniz, because 3 * 20 also 60 and also sums to an element of S0 (23)
6,11 not decideable by Leibniz, because 2 * 33 also 66 and also sums to an element of S0 (35)
7,10 not decideable by Leibniz, because 2 * 35 also 70 and also sums to an element of S0 (37)
8,9 not decideable by Leibniz, because 3 * 24 also 72 and also sums to an element of S0 (27)So we have an answer. x,y = (4,13)
Is it unique? You might think we have to do the same exercise we just did for 17 with 29, 41, and 53 which have far more pairs and therefore would be far more tedious. But you don't need to look at all pairs, just find 2 that are 'decidable by Leibniz'. Remember we already have a shortcut to finding one that is 'decidable by Leibniz', namely a prime + a multiple of 2. We only need to poke around to find one more.
If you do that you get (one possible answer anyway):
29: (16, 13) and (4,25) are both 'decidable by Leibniz'
41: (4,37) and (3,38) are both 'decidable by Leibniz'
53: (6,47) and (16,37) are both 'decidable by Leibniz'So our original answer pair 4,13 is unique.
@jon-nyc said in Puzzle time - two integers:
Due to Goldbach's conjecture
We all know how much I love to nitpick, hence let me point out that you don't need the Goldbach conjecture. Your method would work even if the conjecture turns out to be false.
-
@jon-nyc said in Puzzle time - two integers:
Due to Goldbach's conjecture
We all know how much I love to nitpick, hence let me point out that you don't need the Goldbach conjecture. Your method would work even if the conjecture turns out to be false.
True. Let’s say instead “due to all the work done to explore whether Goldbach’s Conjecture is true or not, we can safely say that...”
Since Goldbach’s conjecture has been verified up to ~10^18, and we only need it to hold up to 198, that should work.