Puzzle Time - Pappus Theorum
-
Two lines are drawn, and three points are randomly selected on each line. Straight lines connect the six points, and the three intersections of those lines are marked.
Oddly, the three intersections all lie upon a straight line.
Will this be true in all cases???
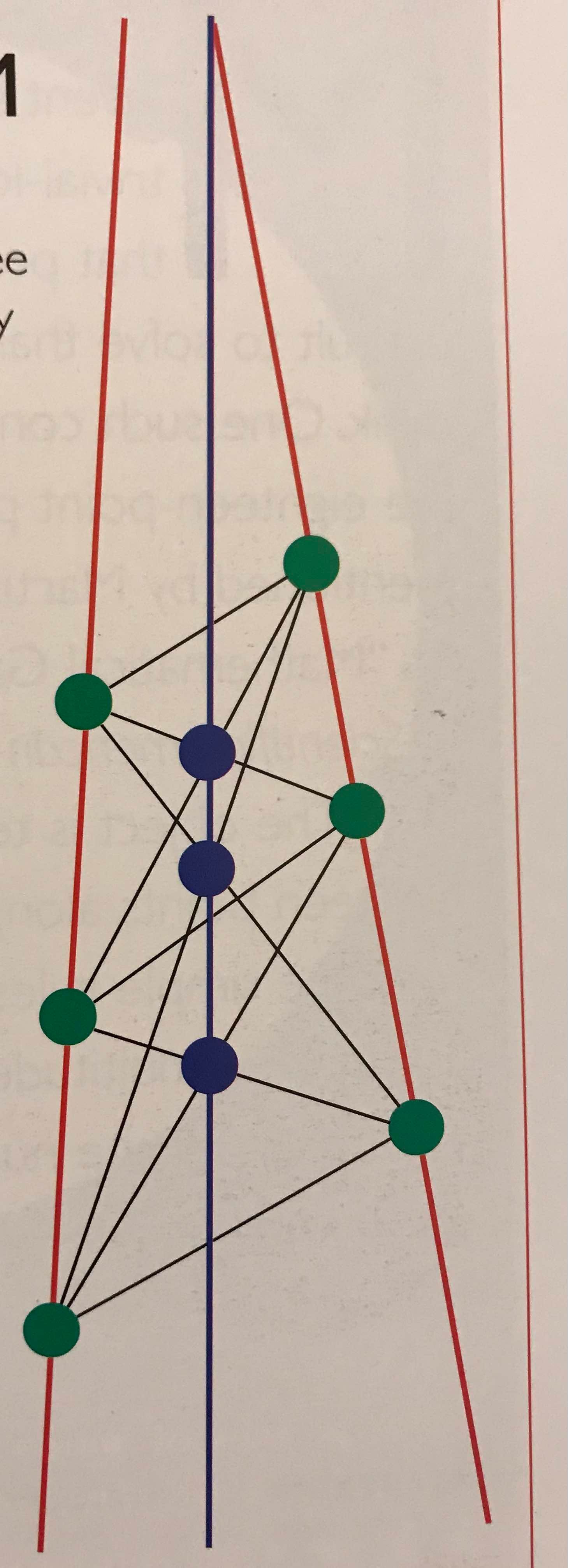
In picture above,
red line = random lines
green dots = random points
blue dots = resulting intersection points
blue line = resulting straight line -
@Axtremus the Random lines that you place the dots on should be straight.
May change things for you.
-
I think Ax's example is fine, but your description isn't quite accurate.
There are more than three intersections if you extend all the lines.
Let's call the points on the first line A,B,C (in order) and on the second line a,b,c.
Then you are only interested in the intersections Ab-bA, Ac-aC, and Bc-bC.
The lines through Aa and Bb, for instance, do also intersect somewhere, but they are not what this puzzle is about.
In Ax's diagram, the three points described above are still on a straight line, but the intersection points may be way outside of the visible part of the diagram.
-
I'm going to be a contrarian and say yes but I can't prove it yet (hence no spoiler).
Notice it isn't all the intersections, it's three out of the seven of them. If you call the points on the first line A, B, and C and the second A', B', and C', with A and A' being closest to the intersection of the main two lines, then the segments of interest are:
AB', AC', BA', BC', CA', CB'.
The segments AA', and CC' don't intersect (except in p=0 cases) and the segment BB' doesn't intersect on the same line as three we care about, except in edge cases.
Klaus - note that when you move a point, it moves two of the lines with it so changes the line made by the three points, but I believe those points still line up. Here's an example where I did just that:
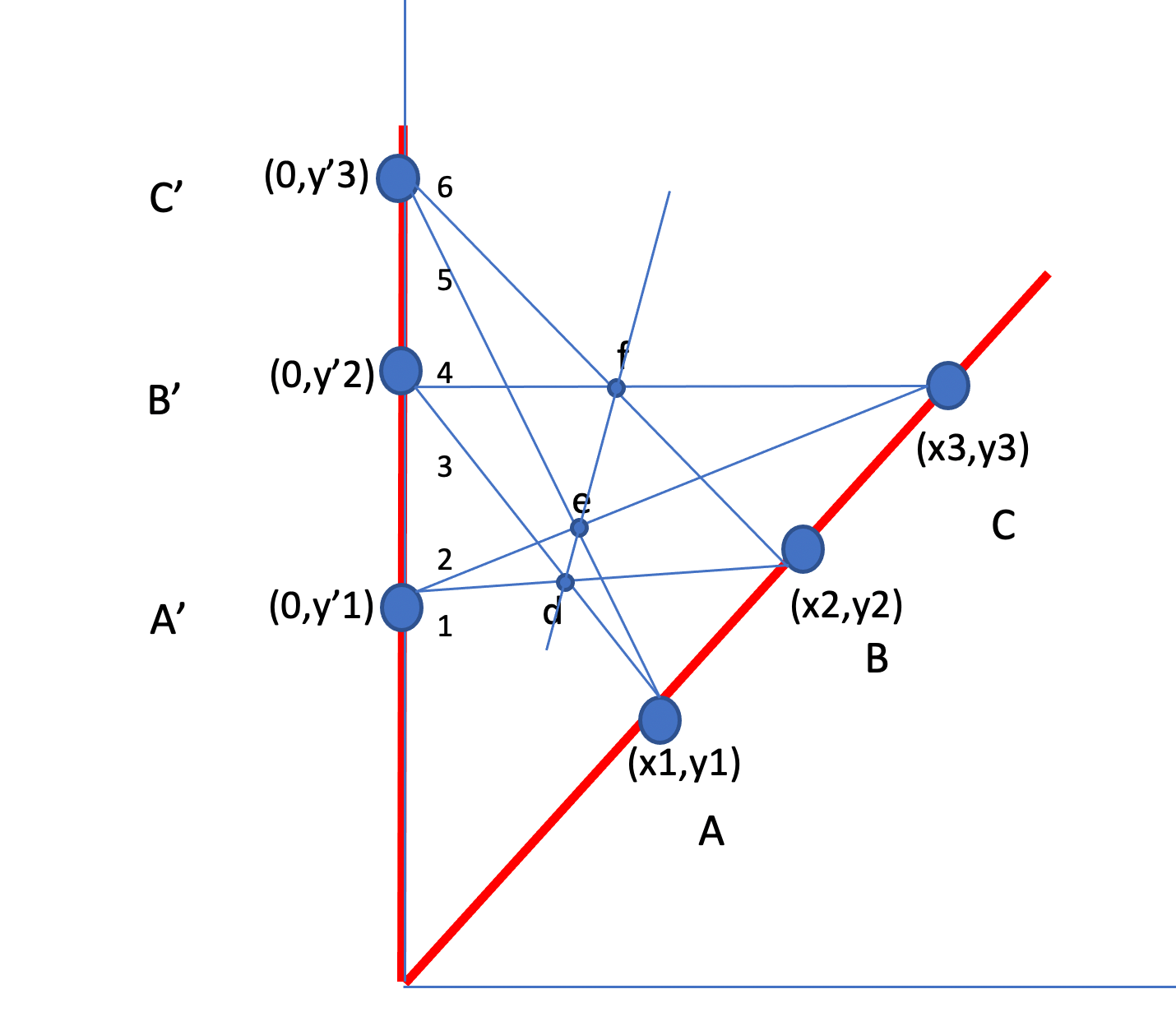
Now I slide point A down, it moves segments 3 (AB') and 5 (AC'). Points e and f both move, but they still appear to line up.
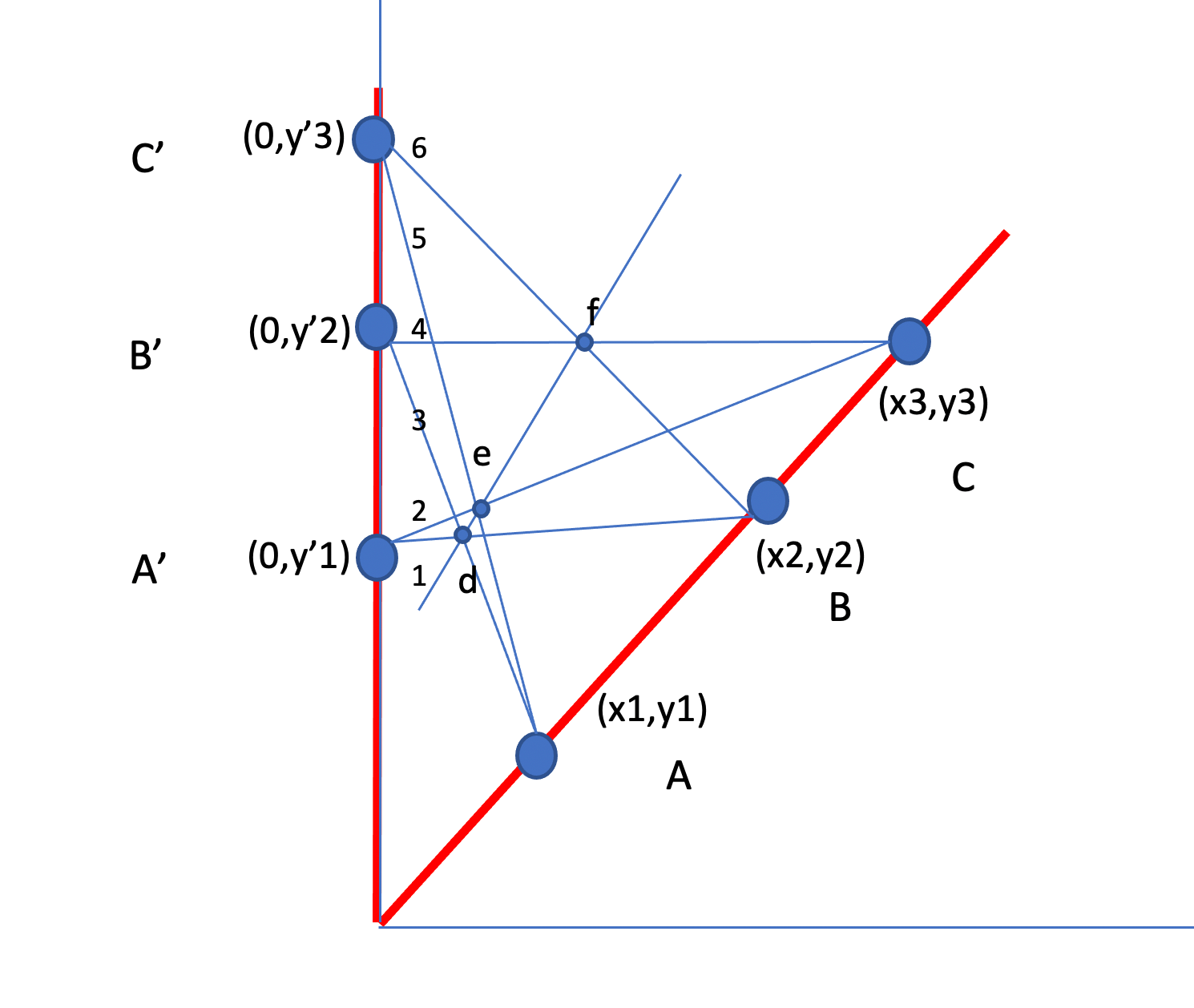
I was trying to prove this by showing that the slopes of the segments (not drawn) de and ef are identical. The equations got really hairy and I either need to improve my handwriting or change my notation to stop me from making several errors per step.
I might continue or explore other ideas for a proof when I have some time.
-
I'm going to be a contrarian and say yes but I can't prove it yet (hence no spoiler).
Notice it isn't all the intersections, it's three out of the seven of them. If you call the points on the first line A, B, and C and the second A', B', and C', with A and A' being closest to the intersection of the main two lines, then the segments of interest are:
AB', AC', BA', BC', CA', CB'.
The segments AA', and CC' don't intersect (except in p=0 cases) and the segment BB' doesn't intersect on the same line as three we care about, except in edge cases.
Klaus - note that when you move a point, it moves two of the lines with it so changes the line made by the three points, but I believe those points still line up. Here's an example where I did just that:

Now I slide point A down, it moves segments 3 (AB') and 5 (AC'). Points e and f both move, but they still appear to line up.

I was trying to prove this by showing that the slopes of the segments (not drawn) de and ef are identical. The equations got really hairy and I either need to improve my handwriting or change my notation to stop me from making several errors per step.
I might continue or explore other ideas for a proof when I have some time.
@jon-nyc said in Puzzle Time - Pappus Theorum:
Klaus - note that when you move a point, it moves two of the lines with it so changes the line made by the three points, but I believe those points still line up.
Yes, which is exactly what I said above

-
Maybe it can be solved for an easy case like the outer lines being at right angles, and then generalized from there?
For example, I could take a physical mock-up of the right angle case and make its projection on a wall be whatever angle I want and it would still be a straight line in the middle.
