Puzzle time - the bent coin
-
Suppose you choose a real number P between 0 and 1 uniformly at random, then make a (bent) coin whose probability of coming up heads when you flip it is P. Finally, you flip this coin 100 times. What is the probability that at the conclusion of this whole experiment, you end up with exactly 50 heads?
-
||I would say zero. But, will give more thought.||
-
@jon-nyc said in Puzzle time - the bent coin:
Seems like it should vary with P, no?
The way you phrased it I'd say "no".
You said P is chosen uniformly from [0,1], so the probability for 50 heads should integrate over all possible choices of P, which means that it doesn't depend on a particular choice of P. That's the reason for the integral in my formula. If you want just the formula for a fixed P, remove the integral and replace "x" by "P". But if you meant that, then the information that P is chosen from a uniform distribution would be meaningless.
-
@jon-nyc said in Puzzle time - the bent coin:
Seems like it should vary with P, no?
The way you phrased it I'd say "no".
You said P is chosen uniformly from [0,1], so the probability for 50 heads should integrate over all possible choices of P, which means that it doesn't depend on a particular choice of P. That's the reason for the integral in my formula. If you want just the formula for a fixed P, remove the integral and replace "x" by "P". But if you meant that, then the information that P is chosen from a uniform distribution would be meaningless.
-
@Moonbat said in Puzzle time - the bent coin:
@Klaus do you need to do that integral? Won't it average out the same as a fair coin?
Hey Moonbat, good to "see" you again! How are things?
It won't average out the same as a fair coin, because the probability is highest when the coin is fair and gets lower the more biased it is.
-
This is an identical problem:
Randomly generate 100 numbers uniformly distributed between 0 and 1
Now randomly generate a 101st number between 0 and 1 the same way (call this number p). This is your boundary. Of the first hundred numbers you generated, the numbers lower than p we call heads, the numbers higher we call tails.
But it's clear that the 101st number is no more likely to be between any one adjacent pair of the first 100 than any of the other adjacent pairs.
Ergo the probability of all the different numbers of heads are identical. Those range from 0 to 100, so 101 options.
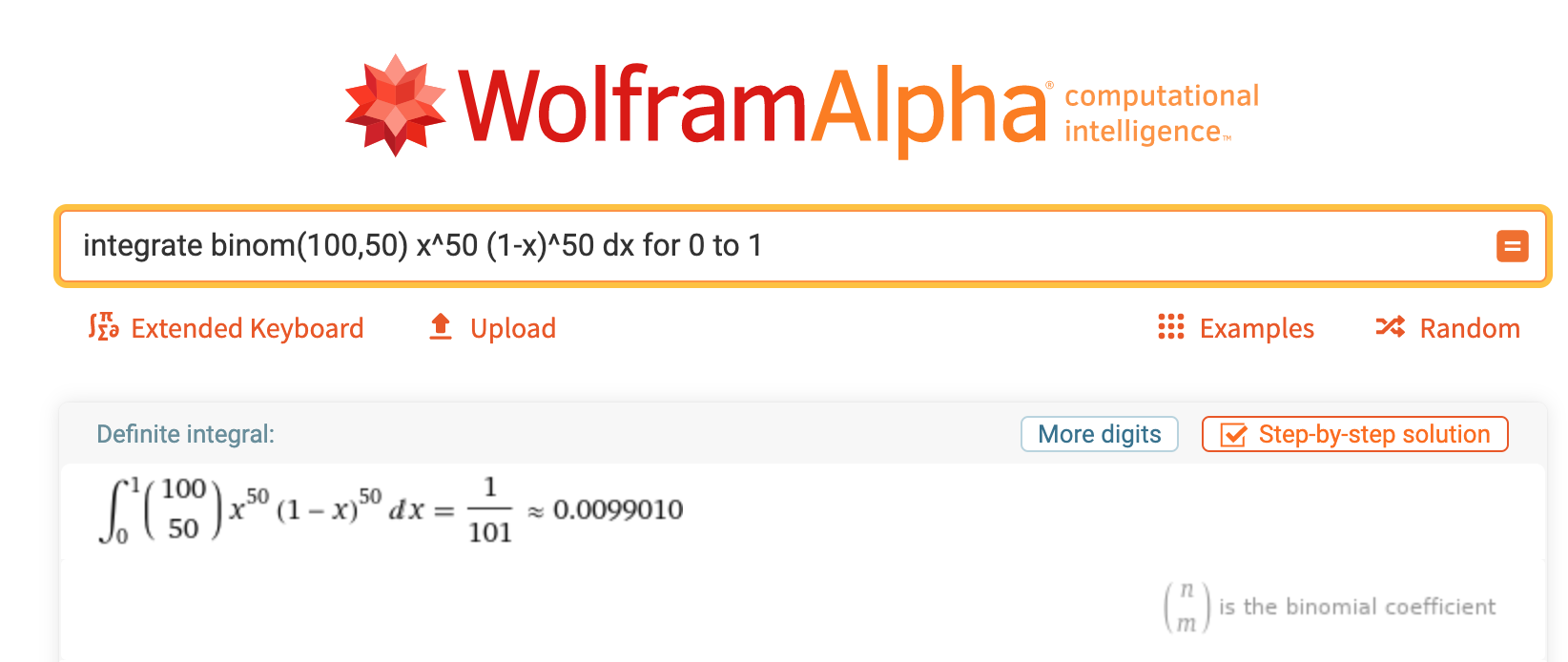
So Klaus's answer is correct. 1/101
(Perhaps counter intuitively, the odds of getting 100 consecutive heads or 100 consecutive tails are also 1/101)
-
This is an identical problem:
Randomly generate 100 numbers uniformly distributed between 0 and 1
Now randomly generate a 101st number between 0 and 1 the same way (call this number p). This is your boundary. Of the first hundred numbers you generated, the numbers lower than p we call heads, the numbers higher we call tails.
But it's clear that the 101st number is no more likely to be between any one adjacent pair of the first 100 than any of the other adjacent pairs.
Ergo the probability of all the different numbers of heads are identical. Those range from 0 to 100, so 101 options.
So Klaus's answer is correct. 1/101
(Perhaps counter intuitively, the odds of getting 100 consecutive heads or 100 consecutive tails are also 1/101)
@jon-nyc said in Puzzle time - the bent coin:
But it's clear that the 101st number is no more likely to be between any one adjacent pair of the first 100 than any of the other adjacent pairs.
What do you mean by "between"? Do you assume that the 100 numbers are ordered?
the probability of all the different numbers of heads are identical.
What does that sentence mean? Events have a probability. What is the event there?
If I understand correctly, you assume that the numbers are ordered and then you consider which pair of adjacent numbers in that ordering is such that p fits in between those numbers. While the probability to fit between a particular pair is not the same as for any other pair for a given set of 100 numbers, it is the same in the a priori situation when the 100 numbers are not known yet.
That makes sense. Nice solution. Certainly way simpler, and more insightful, than mine.
-
This is an identical problem:
Randomly generate 100 numbers uniformly distributed between 0 and 1
Now randomly generate a 101st number between 0 and 1 the same way (call this number p). This is your boundary. Of the first hundred numbers you generated, the numbers lower than p we call heads, the numbers higher we call tails.
But it's clear that the 101st number is no more likely to be between any one adjacent pair of the first 100 than any of the other adjacent pairs.
Ergo the probability of all the different numbers of heads are identical. Those range from 0 to 100, so 101 options.
So Klaus's answer is correct. 1/101
(Perhaps counter intuitively, the odds of getting 100 consecutive heads or 100 consecutive tails are also 1/101)
@jon-nyc For your question here, is there a "limit" on the number of decimal point for the 100 numbers or does it not matter?
For example, could one number be 0.1 and another be 0.100000001?