Puzzle time - but not so hard
-
Players A and B alternately place a checker on an unoccupied square of an initially empty eight-by-eight checkerboard. The rule is that after A places his initial checker, every new checker must be (orthogonally) adjacent to the most recently placed checker. The players are in effect constructing a path of checkers. The last player to make a legal move wins the game.
For illustration, here's an example game where A beats B.
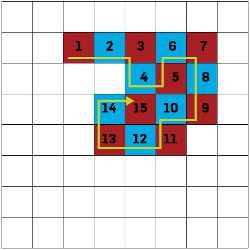
Your mission: find a winning strategy for B.
When you got that figured out, here's a little extension of the puzzle.
Suppose that A, when it is his turn, is no longer obliged to play next to B's last checker and may instead place his checker on any unoccupied square. B is still constrained to "match" A, that is, to play next to A's last move. As in the Path Game, the last player to make a legal move wins the game. So who wins now, with best play?