Geometry problems, v2
-
My problem is about constructing with compass and straight-edge.
The rules of these constructions are simple. The straight-edge has no scale/numbers. You can connect dots or intersections with the straight-edge, or extend an existing line. You can draw circles of arbitrary radius. In particular, you can draw a circle starting from two given points: the centre and a point on the circle. No "trying out until it fits" allowed. You can assume that the compass keeps its radius unless you change it, that is, you can draw multiple circles of the same radius.
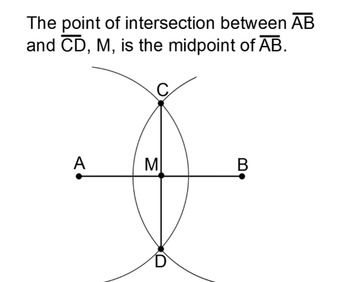
Today we want to look at division. Here's how to divide by two, i.e., how to divide the line segment AB into two segments of equal length.
Here's my challenge: Divide by three!
-
I know a method that involves constructing a new line segment off of one of the end points, using a compass to make three adjacent circles on that segment (this trisecting that segment) and forming a triangle with the original segment and trisected segment. You can then make new connections from the trisected segment to the original and, if parallel to the base of the large triangle, they’ll trisect the original segment.
-
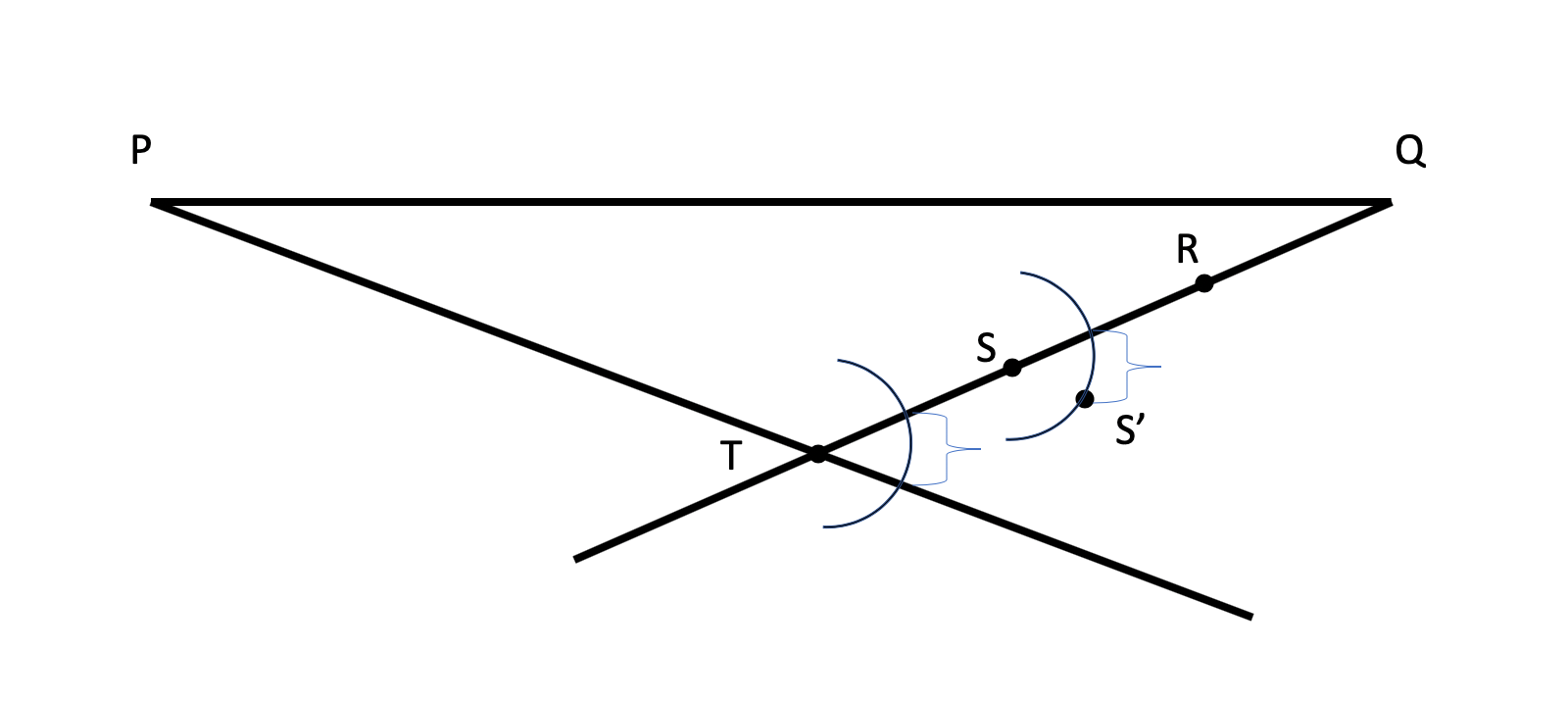
Ok, original line segment is PQ. Draw a segment starting at Q as shown. Put an arbitrary point R on it. Use R as the center and make a circle with radius QR. Define the point S where the circle intersects with the segment. Then move your compass to center on S which gives you point T. R and S now trisect QT.
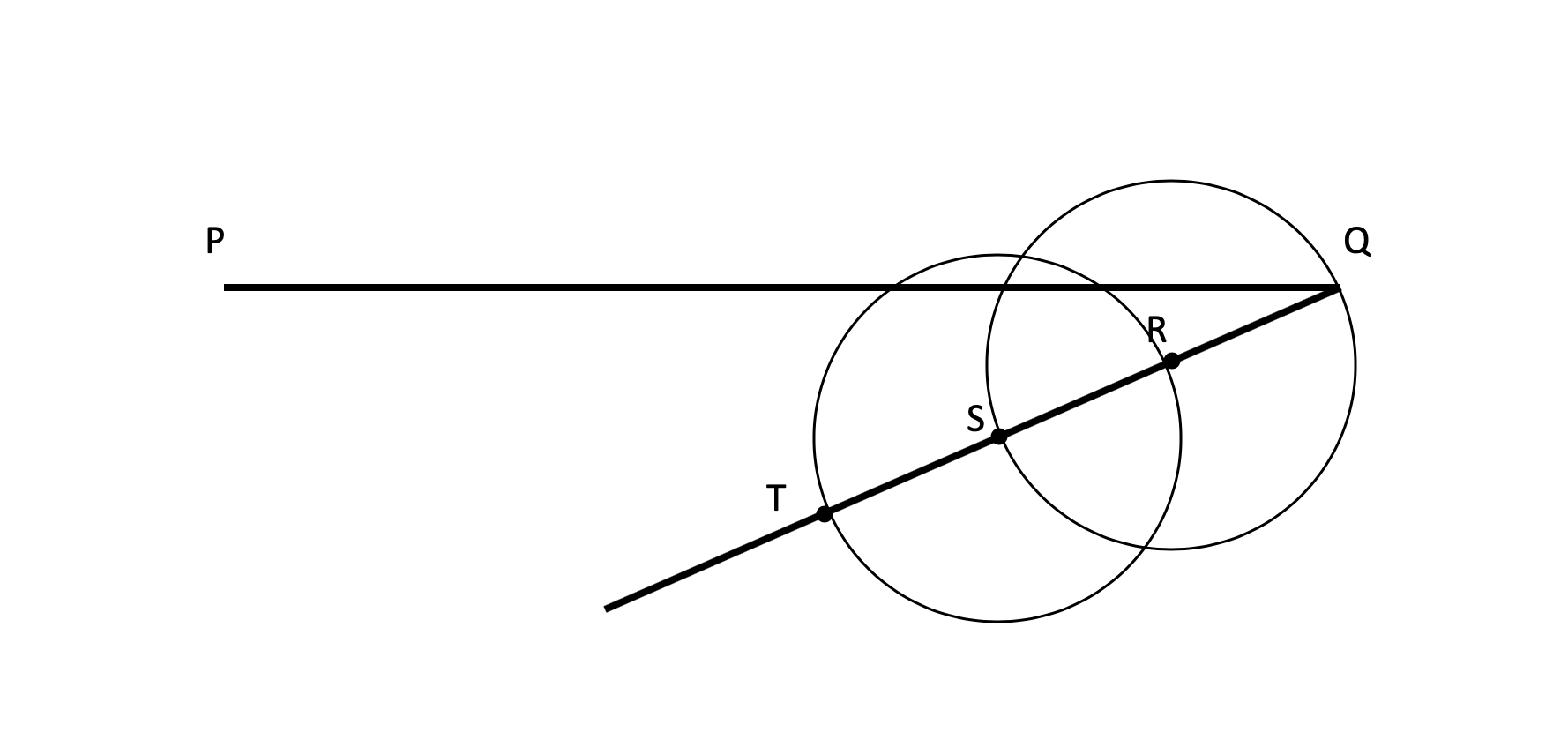
Next, draw PT with your straightedge.
Now draw a circle centered on S for which the extension of PT is a tangent. Draw a new circle with the same radius that also has PT as a tangent a little closer to P. The line formed by the centers of the two circles will intersect PQ at a trisection point. Repeat with R.
-
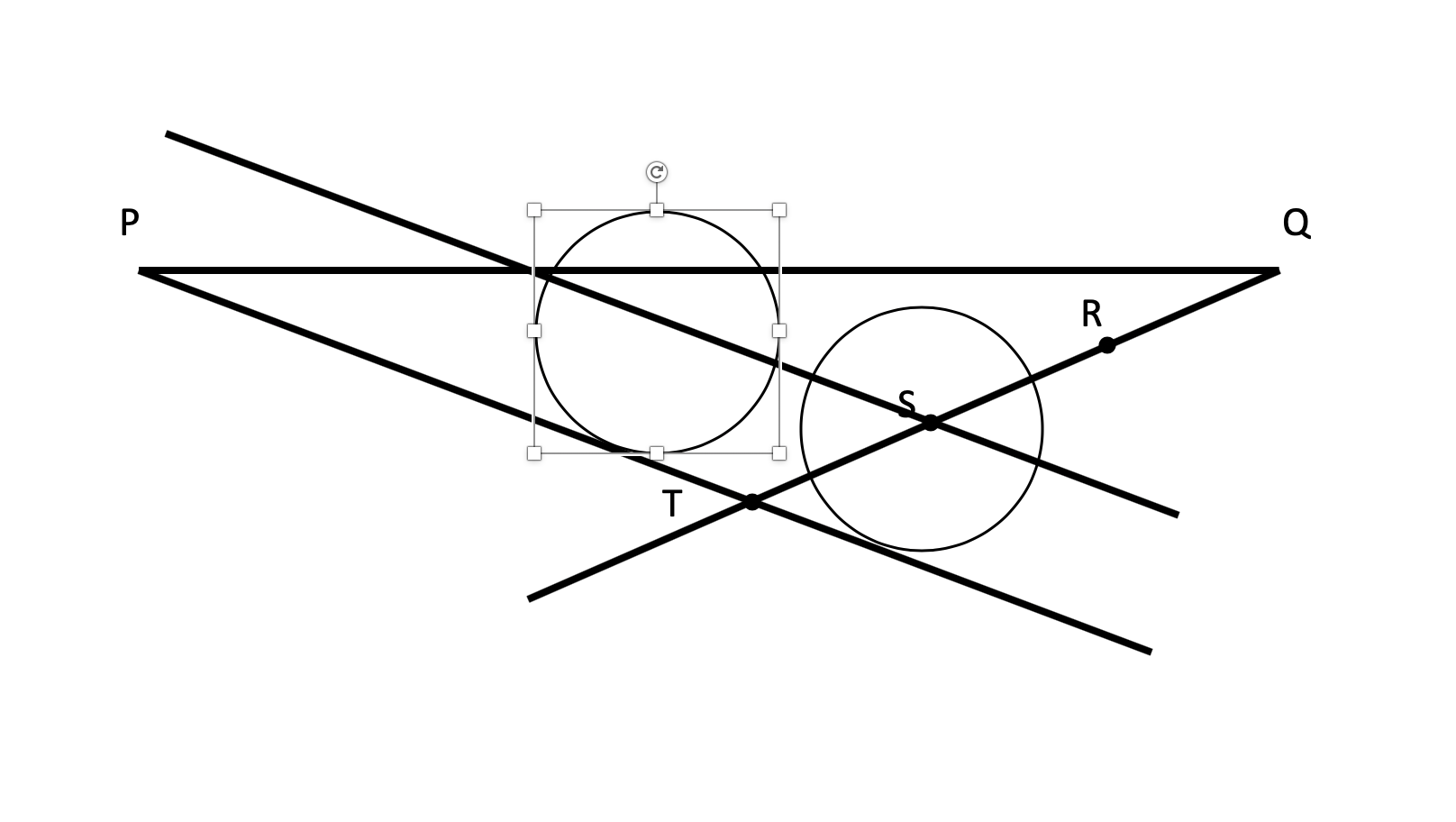
Ok, original line segment is PQ. Draw a segment starting at Q as shown. Put an arbitrary point R on it. Use R as the center and make a circle with radius QR. Define the point S where the circle intersects with the segment. Then move your compass to center on S which gives you point T. R and S now trisect QT.

Next, draw PT with your straightedge.
Now draw a circle centered on S for which the extension of PT is a tangent. Draw a new circle with the same radius that also has PT as a tangent a little closer to P. The line formed by the centers of the two circles will intersect PQ at a trisection point. Repeat with R.

You are definitely on the right track, but this:
@jon-nyc said in Geometry problems, v2:
Now draw a circle centered on S for which the extension of PT is a tangent. Draw a new circle with the same radius that also has PT as a tangent a little closer to P.
falls under the "trying out until it fits" criterion I described above: it's not a geometric construction. Circles can only be drawn starting from two given points: the centre and a point on the circle. Both points need to be fixed before you draw the circle.
You also cannot construct a parallel line by drawing two distinct circles of the same radius with centers on the line and then use the straightedge to draw a tangent that is parallel to the line. As I said above, you can only connect dots or intersections with the straight-edge, or extend an existing line.
Isn't it fascinating that this kind of math is 2300 years old? And there's still loads of open problems even today.
-
Fair enough.
So use this method for the parallel line:
Draw a small arc around point T. Using same radius do another around S. Using the compass, measure the distance between the points of the arc where it intersects PT and TQ. Measuring the same distance on the other arc from where it intersects TQ will give you a point S'. The angle RSS' Is the same as the angle formed around T, hence the line SS' is parallel to PT. It will intersect PQ at a trisection point.