Puzzle time - cover the square with circles

[jon-nyc]

Suppose you have a unit square. If you also have four identical circles that can overlap, they would need to have a radius of 0.25·√2 to completely cover the square, as shown:

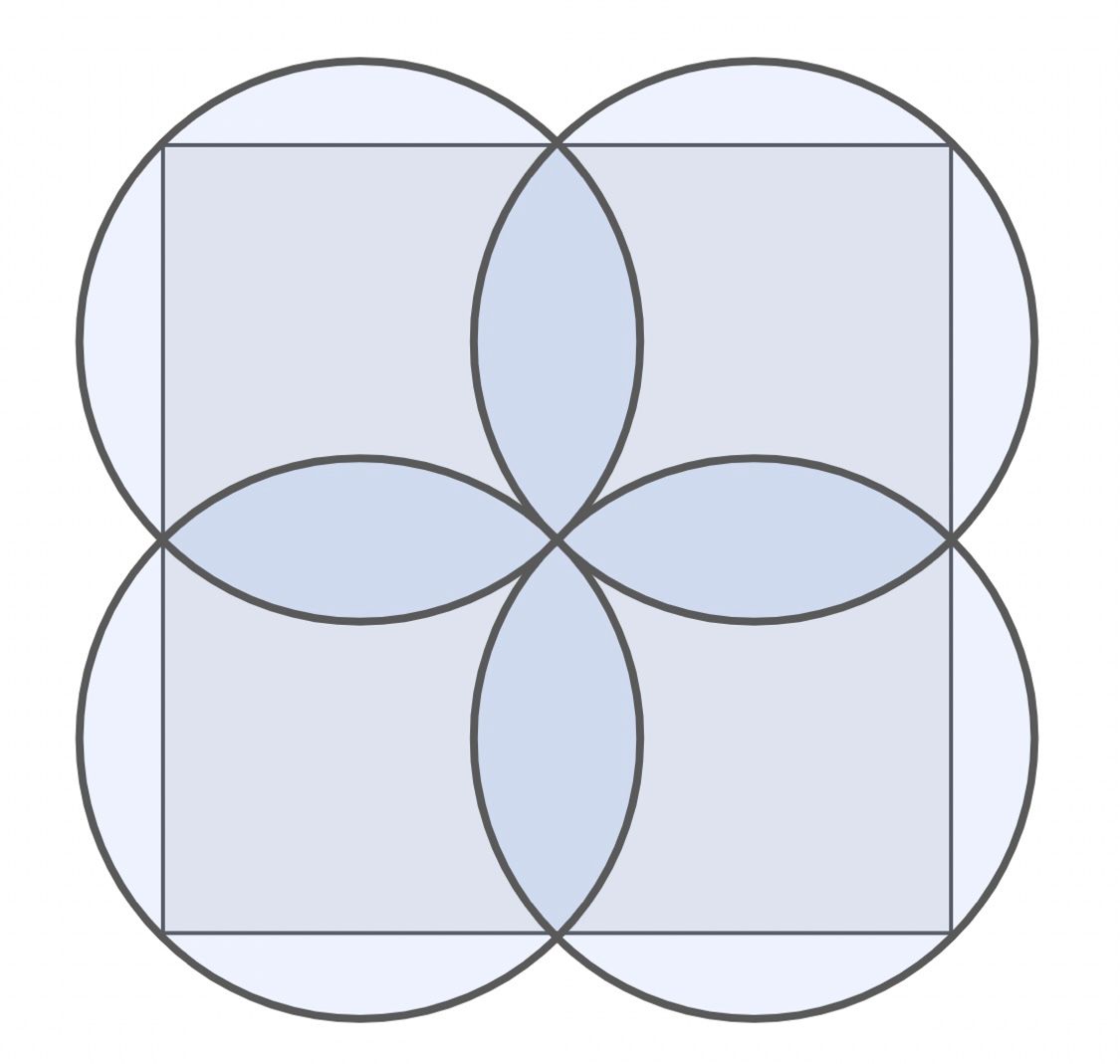
Now suppose that, instead of four identical circles, you have five identical circles that can overlap. What is the minimum radius they would need to completely cover a unit square?

Extra credit: Suppose you have six identical circles that can overlap. What is the minimum radius they would need to completely cover a unit square?

[Mik]

Fucking geometry.

[Klaus]

Hm, I don't find it obvious that the fifth circle even helps.

So let me put out the null hypothesis that the needed radius is still 0.25·√2

[Klaus]

OK, I accidentally stumbled upon the solution in a 1997 math paper...