Puzzle time - Pi = 4
-
We know that the circumference of a circle of radius 1 is 2*Pi.
I'm going to prove that the circumference of that circle is 8, hence Pi = 4.
To this end, I construct a series of lines that give better and better approximations of the circle.
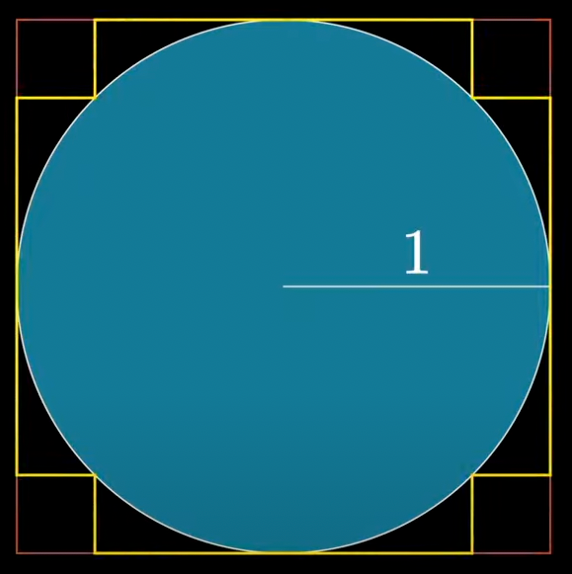
I start with the square around the circle. Clearly it has length 4. Let's call this s-1.
Then I fold the edges in like in the yellow line here. Let's call this s-2. It still has length 4.
Now I repeat this process of folding in the edges, giving better and better approximations of the circle.
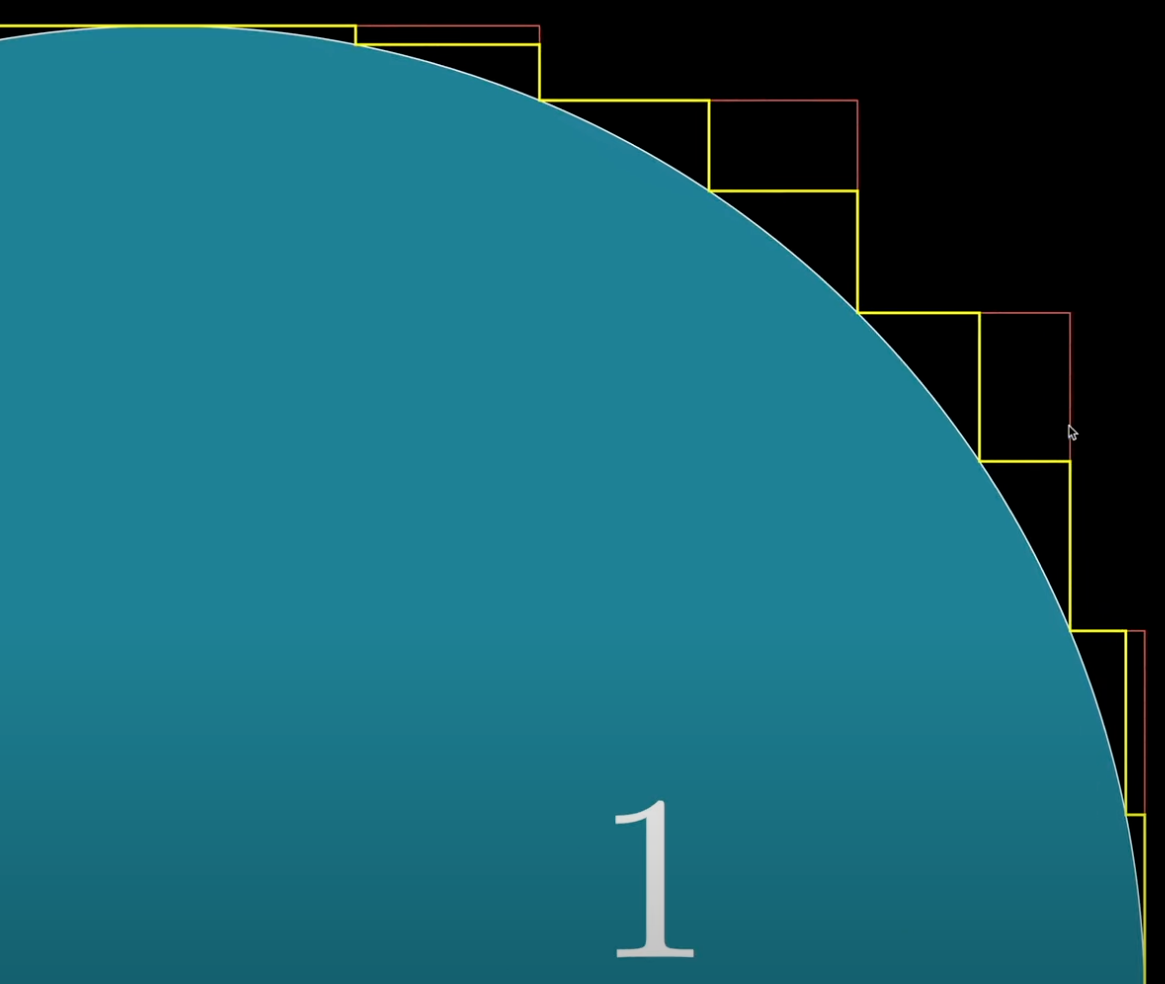
The limit of s-n, as n goes to infinity literally is the circle: It's distance from the circle is 0 at every point.
Also, the limit of the length of s-n as n goes to infinity is 4 - which is trivial, since the length of each s-i is 4.
Hence Pi = 4.
Where's the error in this proof?
-
We know that the circumference of a circle of radius 1 is 2*Pi.
I'm going to prove that the circumference of that circle is 8, hence Pi = 4.
To this end, I construct a series of lines that give better and better approximations of the circle.
I start with the square around the circle. Clearly it has length 4. Let's call this s-1.
Then I fold the edges in like in the yellow line here. Let's call this s-2. It still has length 4.
Now I repeat this process of folding in the edges, giving better and better approximations of the circle.
The limit of s-n, as n goes to infinity literally is the circle: It's distance from the circle is 0 at every point.
Also, the limit of the length of s-n as n goes to infinity is 4 - which is trivial, since the length of each s-i is 4.
Hence Pi = 4.
Where's the error in this proof?
@Klaus said in Puzzle time - Pi = 4:
We know that the circumference of a circle of radius 1 is 2*Pi.
I'm going to prove that the circumference of that circle is 8, hence Pi = 4.
To this end, I construct a series of lines that give better and better approximations of the circle.
I start with the square around the circle. Clearly it has length 4. Let's call this s-1.
Then I fold the edges in like in the yellow line here. Let's call this s-2. It still has length 4.
Now I repeat this process of folding in the edges, giving better and better approximations of the circle.
The limit of s-n, as n goes to infinity literally is the circle: It's distance from the circle is 0 at every point.
Also, the limit of the length of s-n as n goes to infinity is 4 - which is trivial, since the length of each s-i is 4.
Hence Pi = 4.
Where's the error in this proof?
Shit son, I posted this in the OG TNCR way back in the day.
-
I guess the formal answer is to actually do the arithmetic on the Riemann sums. The area under the triangular approximations converges to zero but the ratio of the path lengths stays constant.
-
I guess the formal answer is to actually do the arithmetic on the Riemann sums. The area under the triangular approximations converges to zero but the ratio of the path lengths stays constant.
@jon-nyc said in Puzzle time - Pi = 4:
I guess the formal answer is to actually do the arithmetic on the Riemann sums. The area under the triangular approximations converges to zero but the ratio of the path lengths stays constant.
Nope. I made an error in my "proof" that can be pointed out quite succinctly and precisely.
