Puzzle time - concatenary palindromes
-
Call a number "concatenary" if it is the concatenation of integers (written in base 10) from 1 to some larger integer. For example, 12 and 21 are concatenary; so are 132, 42153, and 129631185210741. To see that this last one qualifies, we space it out like this: 12 9 6 3 11 8 5 2 10 7 4 1.
A number is a "palindrome" if it reads the same forwards and backwards, e.g., 7, 77, 747, 7447, or 2503361633052.
What is the least number that is a concatenary palindrome?
-
124 is not concatenary neither is 111 Ax
The puzzle phrases it vaguely but it has to be a concatenation of consecutive numbers (though ordered any which way) otherwise as you point out it includes every positive integer.
So 1, 2, 3, 4……n but ordered any which way.
-
Coding is quicker than thinking, and this is just a 3-liner:
toStr = foldl (++) "" . map show flt = filter ((\l -> l == reverse l) . toStr) putStr $ show $ concatMap (\n -> flt (permutations [1..n])) [3..]Unfortunately, it has been running for 10min (exhausting the search space until n=12 or n=13 or so) without giving me a palindrome
 So, if there's a palindrome, it must be big.
So, if there's a palindrome, it must be big. -
OK, I turned my little 3-liner into a small back-tracking algorithm which stops early when a solution is no longer feasible, and it scales to n=19.
It turns out that there are 362,880 different palindromes one can make with 1..19.
And indeed the smallest one is the one Jon produced:
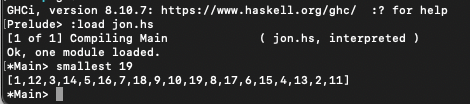
-
Interestingly, my algorithm can produce palindromes very quickly for up to n=22, but at n=23 there is suddenly a problem. The computer hasn't found anything in 10min or so. I assume the third "3" makes it impossible. Which raises the question: What is the set of numbers for which there are palindromes as described above. So far, we know that the
set includes the numbers 19 to 22 but not 2 to 18. -
Interestingly, my algorithm can produce palindromes very quickly for up to n=22, but at n=23 there is suddenly a problem. The computer hasn't found anything in 10min or so. I assume the third "3" makes it impossible. Which raises the question: What is the set of numbers for which there are palindromes as described above. So far, we know that the
set includes the numbers 19 to 22 but not 2 to 18. -
SOLUTION: Suppose that our solution concatenates the numbers from 1 to N. Then each of the digits 1, 2, ..., 9, 0 must appear an even number of times in the numbers from 1 to N, with at most one exception, in order for those digits to be arrangeable into a palindrome.
So a natural first task is to determine the least N with this property, and it turns out to be 19. The numbers from 1 to 19 contain 12 1's, 2 of each digit from 2 to 9, and just one 0 (which would thus have to be in the middle of our concatenary palindrome).
We don't know yet whether there is a concatenary palindrome made from the numbers 1 through 19, but let's be optimistic and try to construct the smallest one we can. We'd want to start the number with the digit 1, and thus it must also end with 1. Can we begin it with two 1's? Yes, but only if we end it with the number eleven, and begin it with the number 1 followed by something in the teens. So our number looks like "1 1x ... 0 ... x 11" for some digit x. So far so good.
We can't have x = 1, but x = 2 is OK, so our number becomes "1 12 y ... 0 ... y 2 11" for some digit y. Can y be 1? No, because the y on the right side can only belong to the number one or the number eleven and we've already used those. But it can be 3, provided that on the right it's part of the number 13. So now we have "1 12 3 1z ... 0 ... z 13 2 11," where z is some digit — which can be taken to be 4.
Proceeding in this manner we end up with
1 12 3 14 5 16 7 18 9 10 19 8 17 6 15 4 13 2 11,
also known as 11,231,451,671,891,019,817,615,413,211, or "eleven octillion something."